
分析 (1)利用绝对值不等式,即可求实数t的最大值s;
(2)若正实数a,b满足4a+5b=s,利用柯西不等式求y=$\frac{1}{a+2b}$+$\frac{4}{3a+3b}$的最小值.
解答 解:(1)因为|2x+5|+|2x-1|-t≥0,所以|2x+5|+|2x-1|≥t,
又因为|2x+5|+|2x-1|≥|2x+5-2x+1|=6,所以t≤6,
所以实数t的最大值s=6.
(2)$\frac{1}{a+2b}$+$\frac{4}{3a+3b}$=$\frac{1}{6}$($\frac{1}{a+2b}$+$\frac{4}{3a+3b}$)(4a+5b)
≥$\frac{1}{6}$$(\sqrt{\frac{1}{a+2b}}•\sqrt{a+2b}+\sqrt{\frac{4}{3a+3b}}•\sqrt{3a+3b})^{2}$=$\frac{3}{2}$
当且仅当a=b=$\frac{2}{3}$时取等号,
所以y=$\frac{1}{a+2b}$+$\frac{4}{3a+3b}$的最小值为$\frac{3}{2}$.
点评 本题考查绝对值不等式,考查柯西不等式的运用,属于中档题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{{\sqrt{2}-\sqrt{6}}}{4}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
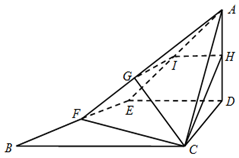 △ABC为等腰直角三角形,AC=BC=4,∠ACB=90°,D、E分别是边AC和AB的中点,现将△ADE沿DE折起,使面ADE⊥面DEBC,H、F分别是边AD和BE的中点,平面BCH与AE、AF分别交于I、G两点
△ABC为等腰直角三角形,AC=BC=4,∠ACB=90°,D、E分别是边AC和AB的中点,现将△ADE沿DE折起,使面ADE⊥面DEBC,H、F分别是边AD和BE的中点,平面BCH与AE、AF分别交于I、G两点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{2}$) | B. | (-∞,1) | C. | ($\frac{1}{2}$,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
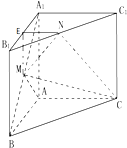 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,点M、N、E分别为A1B、B1C1、A1B1上的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,点M、N、E分别为A1B、B1C1、A1B1上的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com