
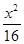
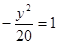 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,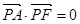
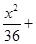
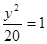 ;(2)点P的坐标为
;(2)点P的坐标为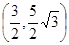 ;
;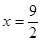 时,d取最小值
时,d取最小值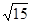 。
。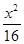
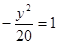 的焦点、顶点,得出椭圆的a,c,b即可求出椭圆标准方程.
的焦点、顶点,得出椭圆的a,c,b即可求出椭圆标准方程.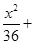
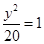 ,与(x+6)(x-4)+y2=0
,与(x+6)(x-4)+y2=0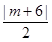 =|m-6|,解出m=2,建立椭圆上的点到M的距离d的表达式,用函数知识求最值。
=|m-6|,解出m=2,建立椭圆上的点到M的距离d的表达式,用函数知识求最值。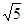 ,半焦距c1=
,半焦距c1=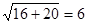 ,
,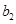 =
=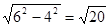 ,
,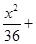
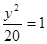 …………4分
…………4分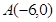 ,
,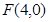 ,设点P的坐标为
,设点P的坐标为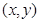 ,则
,则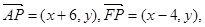 由已知得
由已知得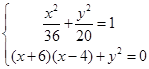 …………6分
…………6分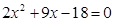 ,解之得
,解之得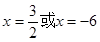 ,
, 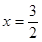 ,于是
,于是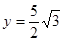 ,所以点P的坐标为
,所以点P的坐标为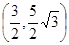 ……8分
……8分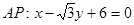 ,设点M是
,设点M是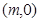 ,则点M到直线AP的距离是
,则点M到直线AP的距离是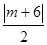 ,于是
,于是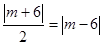 ,
,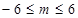
 …………10分
…………10分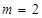 时,椭圆上的点到
时,椭圆上的点到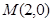 的距离
的距离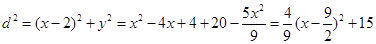
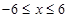 ∴当
∴当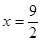 时,d取最小值
时,d取最小值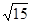 …………12分
…………12分

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源:不详 题型:填空题
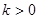 ,则方程
,则方程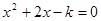 有实根;
有实根;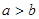 ,则
,则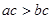 ”的否命题;
”的否命题;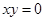 ,则
,则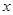 、
、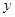 至少有一个为零”的逆否命题 .
至少有一个为零”的逆否命题 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com