
【题目】如图,三棱柱![]() 中,四边形
中,四边形![]() 四边均相等,点
四边均相等,点![]() 在面
在面![]() 的射影为
的射影为![]() 中点
中点![]() .
.

(1)证明:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 点到面
点到面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由点![]() 在面
在面![]() 的射影为
的射影为![]() 中点
中点![]() 可得
可得![]() ,由菱形的性质可得
,由菱形的性质可得![]() ,利用线面垂直的判定定理可得
,利用线面垂直的判定定理可得![]() 平面
平面![]() ,从而可得结果;(2)在平面
,从而可得结果;(2)在平面![]() 内作
内作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,在平面
,在平面![]() 内作
内作![]() ,垂足为
,垂足为![]() .可证明
.可证明![]() 平面
平面![]() ,进而可得结果.
,进而可得结果.
(1)证明 连接BC1,则O为B1C与BC1的交点.
因为侧面BB1C1C为菱形,所以B1C⊥BC1.
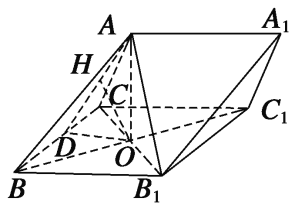
又AO⊥平面BB1C1C,所以B1C⊥AO,
故B1C⊥平面ABO.
由于AB平面ABO,故B1C⊥AB.
(2)在平面BB1C1C内作OD⊥BC,垂足为D,连接AD.
在平面AOD内作OH⊥AD,垂足为H.
由于BC⊥AO,BC⊥OD,
故BC⊥平面AOD,所以OH⊥BC.
又OH⊥AD,
所以OH⊥平面ABC.
因为∠CBB1=60°,所以△CBB1为等边三角形.
又BC=1,可得![]() .由于AC⊥AB/span>1,所以
.由于AC⊥AB/span>1,所以![]() .
.
由OH·AD=OD·OA,且![]() ,得
,得![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】若lg(3x)+lg y=lg(x+y+1),则xy的最小值为( )
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】
先根据对称的运算性质化简得到3xy=x+y+1,再根据基本不等式即可求出答案.
∵lg(3x)+lgy=lg(3xy)=lg(x+y+1),x>0,y>0,
∴3xy=x+y+1,
∴3xy≥3![]() ,当且仅当x=y=1时取等号,
,当且仅当x=y=1时取等号,
即xy≥1,
∴xy的最小值是1,
故选:A
【点睛】
在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误
【题型】单选题
【结束】
12
【题目】已知两定点![]() ,如果动点
,如果动点![]() 满足
满足![]() ,则点
,则点![]() 的轨迹所包围的图形的面积等于( )
的轨迹所包围的图形的面积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面四边形ABCD中,AB=5![]() , ∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.
, ∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.
(I)求AC的长;
(Ⅱ)求CD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2﹣alnx,a∈R.
(1)讨论函数f(x)的单调性;
(2)当a>0时,若f(x)的最小值为1,求a的值;
(3)设g(x)=f(x)﹣2x,若g(x)在[![]() ,
, ![]() ]有两个极值点x1 , x2(x1<x2),证明:g(x1)﹣g(x2)的取值范围.
]有两个极值点x1 , x2(x1<x2),证明:g(x1)﹣g(x2)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的一个焦点为![]() ,对应于这个焦点的准线方程为
,对应于这个焦点的准线方程为![]()
(1)写出抛物线![]() 的方程;
的方程;
(2)过![]() 点的直线与曲线
点的直线与曲线![]() 交于
交于![]() 两点,
两点,![]() 点为坐标原点,求
点为坐标原点,求![]() 重心
重心![]() 的轨迹方程;
的轨迹方程;
(3)点![]() 是抛物线
是抛物线![]() 上的动点,过点
上的动点,过点![]() 作圆
作圆![]() 的切线,切点分别是
的切线,切点分别是![]() .当
.当![]() 点在何处时,
点在何处时,![]() 的值最小?求出
的值最小?求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】箱中有6张卡片,分别标有1,2,3,…,6。
(1)抽取一张记下号码后不放回,再抽取一张记下号码,求两次之和为偶数的概率;
(2)抽取一张记下号码后放回,再抽取一张记下号码,求两个号码中至少一个为偶数的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:2x-y+6=0和直线l2:x=-1,F是抛物线C:y2=4x的焦点,点P在抛物线C上运动,当点P到直线l1和直线l2的距离之和最小时,直线PF被抛物线所截得的线段长是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sin(x+![]() )(x∈R)的图象上所有点的纵坐标不变横坐标缩小到原来的
)(x∈R)的图象上所有点的纵坐标不变横坐标缩小到原来的![]() , 再把图象上各点向左平移
, 再把图象上各点向左平移![]() 个单位长度,则所得的图象的解析式为( )
个单位长度,则所得的图象的解析式为( )
A.y=sin(2x+![]() )
)
B.y=sin(![]() x+
x+![]() )
)
C.y=sin(2x+![]() )
)
D.y=sin(![]() x+
x+![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点,焦点在![]() 轴上的椭圆过点
轴上的椭圆过点![]() ,且它的离心率
,且它的离心率![]()
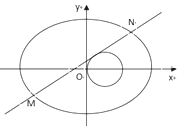
(I)求椭圆的标准方程;
(II)与圆![]() 相切的直线
相切的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,若椭圆上一点
两点,若椭圆上一点![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com