
分析 (I)利用线段的垂直平分线的性质、椭圆的定义即可得出.
(II)设直线l:y=kx+b,F(x1,y1),H(x2,y2)直线l与圆x2+y2=1相切,可得b2=k2+1.直线方程与椭圆方程联立可得:(1+2k2)x2+4kbx+2b2-2=0,△>0,可得k≠0,再利用数量积运算性质、根与系数的关系及其$\frac{3}{4}$≤$\overrightarrow{OF}$•$\overrightarrow{OH}$≤$\frac{4}{5}$,解出即可得出.
解答 解:(I)由题意知MQ中线段AP的垂直平分线,∴$|{CP}|=|{QC}|+|{QP}|=|{QC}|+|{QA}|=2\sqrt{2}>|{CA}|=2$,
∴点Q的轨迹是以点C,A为焦点,焦距为2,长轴为$2\sqrt{2}$的椭圆,$b=\sqrt{{a^2}-{c^2}}=1$,
故点Q的轨迹方程是$\frac{x^2}{2}+{y^2}=1$.
(II)设直线l:y=kx+b,F(x1,y1),H(x2,y2)
直线l与圆x2+y2=1相切$⇒\frac{|b|}{{\sqrt{{k^2}+1}}}=1⇒{b^2}={k^2}+1$
联立$\left\{{\begin{array}{l}{\frac{x^2}{2}+{y^2}=1}\\{y=kx+b}\end{array}}\right.$,(1+2k2)x2+4kbx+2b2-2=0,
△=16k2b2-4(1+2k2)2(b2-1)=8(2k2-b2+1)=8k2>0,可得k≠0,
∴${x_1}+{x_2}=-\frac{4kb}{{1+2{k^2}}},{x_1}{x_2}=\frac{{2{b^2}-2}}{{1+2{k^2}}}$,
$\overrightarrow{OF}•\overrightarrow{OH}={x_1}{x_2}+{y_1}{y_2}=({1+{k^2}}){x_1}{x_2}+kb({x_1}+{x_2})+{b^2}$=$\frac{{(1+{k^2})(2{b^2}-2)}}{{1+2{k^2}}}+kb\frac{(-4kb)}{{1+2{k^2}}}+{b^2}$=$\frac{{(1+{k^2})2{k^2}}}{{1+2{k^2}}}-\frac{{4{k^2}({k^2}+1)}}{{1+2{k^2}}}+{k^2}+1$=$\frac{{1+{k^2}}}{{1+2{k^2}}}$,
∴$\frac{3}{4}≤\frac{{1+{k^2}}}{{1+2{k^2}}}≤\frac{4}{5}$$?\frac{1}{3}≤{k^2}≤\frac{1}{2}$
$⇒\frac{{\sqrt{3}}}{3}≤|k|≤\frac{{\sqrt{2}}}{2}⇒-\frac{{\sqrt{2}}}{2}≤k≤-\frac{{\sqrt{3}}}{3}或\frac{{\sqrt{3}}}{3}≤k≤\frac{{\sqrt{2}}}{2}$为所求.
点评 本题考查了椭圆的标准方程及其性质、直线与圆相切的充要条件、一元二次方程的根与系数的关系、数量积运算性质、不等式的解法,考查了推理能力与计算能力,属于难题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
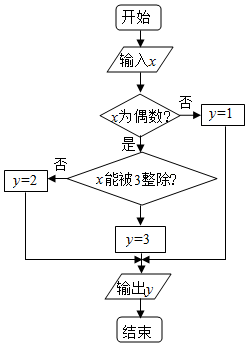 某算法的程序框图如图所示,其中输入的变量z在1,2,3,…,36这36个整数中等可能随机产生,则按程序框图正确编程运行时输出y的值为i的概率Pi(i=l,2,3)分别为( )
某算法的程序框图如图所示,其中输入的变量z在1,2,3,…,36这36个整数中等可能随机产生,则按程序框图正确编程运行时输出y的值为i的概率Pi(i=l,2,3)分别为( )| A. | $\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{6}$ | B. | $\frac{1}{6}$,$\frac{1}{2}$,$\frac{1}{3}$ | C. | $\frac{1}{3}$,$\frac{1}{2}$,$\frac{1}{6}$ | D. | $\frac{1}{2}$,$\frac{1}{6}$,$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{7}{10}$ | D. | $\frac{9}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com