
分析 (1)求出f(x)的导数,计算判别式△,通过讨论a的范围判断函数的单调性;(2)问题转化为-c>6lnx+x2-7x对?x∈(0,6]成立,根据函数恒成立求出c的范围即可.
解答 解:(1)∵f(x)=alnx+x2-8x+c(x>0),
∴f′(x)=$\frac{{2x}^{2}-8x+a}{x}$,…(1分)∴△=64-8a
①当△=64-8a≤0,即a≥8时,f′(x)=$\frac{{2x}^{2}-8x+a}{x}$≥0,
∴f(x)在(0,+∞)上单调递增;…(3分)
②当△=64-8a>0,即0<a<8时,
方程∴f′(x)=$\frac{{2x}^{2}-8x+a}{x}$=0的两根是x1=2-$\frac{\sqrt{16-2a}}{2}$,x2=2+$\frac{\sqrt{16-2a}}{2}$,且0<x1<x2,
∴由f′(x)>0得:0<x<x1或x>x2;
∴f(x)在(0,x1),(x2,+∞)上单调递增;
由f′(x)<0得:x1<x<x2;
∴f(x)在(x1,x2)上单调递减;…(5分)
综上,当a≥8时,f(x)的单调递增区间为(0,+∞);
当0<a<8时,f(x)的递增区间是(0,2-$\frac{\sqrt{16-2a}}{2}$),(2+$\frac{\sqrt{16-2a}}{2}$,+∞),
递减区间是(2-$\frac{\sqrt{16-2a}}{2}$,2+$\frac{\sqrt{16-2a}}{2}$)…(6分)
(2)∵对任意k∈[-1,1],函数y=kx(x∈(0,6])的图象总在函数f(x)=6lnx+x2-8x+c图象的上方,
∴kx>f(x)对?x∈(0,6],?k∈[-1,1]成立…(7分)
∴kx>6lnx+x2-8x+c对?k∈[-1,1]成立,
∴-x>6lnx+x2-8x+c对?x∈(0,6]成立…(9分)
∴-c>6lnx+x2-7x对?x∈(0,6]成立,
令g(x)=6lnx+x2-7x,则g′(x)=$\frac{(2x-3)(x-2)}{x}$,
由g′(x)=0,解得:x=$\frac{3}{2}$或x=2,
∴g($\frac{3}{2}$)=6ln$\frac{3}{2}$-$\frac{33}{4}$<0,
g(2)=6ln2+4-14=6ln2-10<0,
g(6)=6ln6+36-42=6ln6-6>0,
∴g(x)max=g(6)=6ln6-6,
∴-c>6ln6-6,
即c<6-6ln6…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用,函数恒成立问题,本题有一定的难度.


科目:高中数学 来源: 题型:填空题
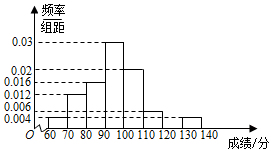 某校在一次期末考试中,全校学生的数学成绩都介于60分到140分之间(满分150分),为了估计该校学生的数学考试情况,从该校2000名学生的数学成绩中随机抽取50名学生的数学成绩,将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140].如图是按照上述分组得到的频率分布直方图的一部分.估计该校2000名学生这次考试的数学成绩的平均分为97.
某校在一次期末考试中,全校学生的数学成绩都介于60分到140分之间(满分150分),为了估计该校学生的数学考试情况,从该校2000名学生的数学成绩中随机抽取50名学生的数学成绩,将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140].如图是按照上述分组得到的频率分布直方图的一部分.估计该校2000名学生这次考试的数学成绩的平均分为97.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y平均增加3.5个单位 | B. | y平均增加2个单位 | ||
| C. | y平均减少3.5个单位 | D. | y平均减少2个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
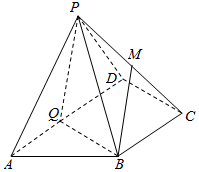 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ADC=90°,AD∥BC,平面PAD⊥底面ABCD,BC=$\frac{1}{2}$AD,PA=PD=AB=2,M,Q为AD,PC的中点
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ADC=90°,AD∥BC,平面PAD⊥底面ABCD,BC=$\frac{1}{2}$AD,PA=PD=AB=2,M,Q为AD,PC的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com