
【题目】选修4-5:不等式选讲
已知函数![]()
(Ⅰ)已知常数![]() 解关于
解关于![]() 的不等式
的不等式![]() ;
;
(Ⅱ)若函数![]() 的图象恒在函数
的图象恒在函数![]() 图象的上方,求实数
图象的上方,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析: (Ⅰ)去掉绝对值结合![]() 即可求出不等式的解集;(Ⅱ)函数
即可求出不等式的解集;(Ⅱ)函数![]() 的图像恒在函数
的图像恒在函数![]() 图像的上方,转化为
图像的上方,转化为![]() 恒成立,分离参变量,利用绝对值不等式求出函数的最值,进而求得参数的范围.
恒成立,分离参变量,利用绝对值不等式求出函数的最值,进而求得参数的范围.
试题解析:(Ⅰ)由![]() 得
得![]() ,所以
,所以![]() 或
或![]()
所以![]() 或
或![]() ,故不等式解集为
,故不等式解集为![]()
(Ⅱ)因为函数![]() 的图像恒在函数
的图像恒在函数![]() 图像的上方,所以
图像的上方,所以![]() 恒成立,则
恒成立,则![]() 恒成立,因为
恒成立,因为![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]()
点睛:本题考查解不等式以及由恒成立问题转化的含绝对值函数的最值问题,属于基础题目. 对绝对值三角不等式:|a|-|b|≤|a±b|≤|a|+|b|.(1)当ab≥0时,|a+b|=|a|+|b|;当ab≤0时,|a-b|=|a|+|b|.(2)该定理可以推广为|a+b+c|≤|a|+|b|+|c|,也可强化为||a|-|b||≤|a±b|≤|a|+|b|,它们经常用于含绝对值的不等式的推证.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
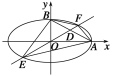
(1)若![]() =6
=6![]() ,求k的值;
,求k的值;
(2)求四边形AEBF面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区工商局、消费者协会在![]() 月
月![]() 号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取
号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取![]() 名群众,按他们的年龄分组:第
名群众,按他们的年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
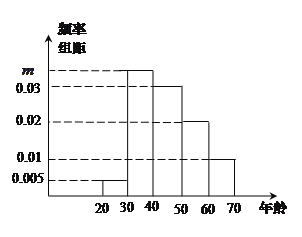
(Ⅰ)若电视台记者要从抽取的群众中选![]() 人进行采访,求被采访人恰好在第
人进行采访,求被采访人恰好在第![]() 组或第
组或第![]() 组的概率;
组的概率;
(Ⅱ)已知第![]() 组群众中男性有
组群众中男性有![]() 人,组织方要从第
人,组织方要从第![]() 组中随机抽取
组中随机抽取![]() 名群众组成维权志愿者服务队,求至少有两名女性的概率.
名群众组成维权志愿者服务队,求至少有两名女性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中公差d≠0,有a1+a4=14,且a1,a2,a7成等比数列.
(Ⅰ)求{an}的通项公式an与前n项和公式Sn;
(Ⅱ)令bn=![]() (k<0),若{bn}是等差数列,求数列{
(k<0),若{bn}是等差数列,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,两焦点
,两焦点![]() ,点
,点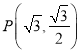 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
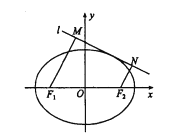
(2)如图,动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,点
有且仅有一个公共点,点![]() 、
、![]() 是直线
是直线![]() 上的两点,且
上的两点,且![]() .求四边形
.求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com