
【题目】已知椭圆![]() 的方程为
的方程为![]() ,两焦点
,两焦点![]() ,点
,点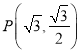 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
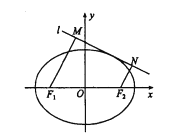
(2)如图,动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,点
有且仅有一个公共点,点![]() 、
、![]() 是直线
是直线![]() 上的两点,且
上的两点,且![]() .求四边形
.求四边形![]() 面积
面积![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)本问考查椭圆标准方程的求法,可以采用待定系数法,即根据已知条件列方程组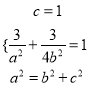 ,解方程组,就可以求出椭圆的方程,另外本题也可以利用椭圆定义求标准方程,即
,解方程组,就可以求出椭圆的方程,另外本题也可以利用椭圆定义求标准方程,即![]() ,根据两点间距离公式,可以求出
,根据两点间距离公式,可以求出![]() 的值,这样也可以得到椭圆标准方程;(2)本问考查直线与椭圆的综合问题,由于直线
的值,这样也可以得到椭圆标准方程;(2)本问考查直线与椭圆的综合问题,由于直线![]() 与椭圆
与椭圆![]() 相切,因此通过联立方程,消元,所得一元二次方程满足判别式
相切,因此通过联立方程,消元,所得一元二次方程满足判别式![]() ,可以得到
,可以得到![]() 之间的关系式,转化为关于一个变量的问题,接下来分别求出两焦点到直线
之间的关系式,转化为关于一个变量的问题,接下来分别求出两焦点到直线![]() 的距离
的距离![]() ,根据四边形
,根据四边形![]() 的面积为
的面积为![]() ,于是问题转化为求
,于是问题转化为求![]() 的值,由图形,过点
的值,由图形,过点![]() 向
向![]() 作垂线,垂足为
作垂线,垂足为![]() ,则
,则![]() ,而
,而![]() ,于是可以将四边形
,于是可以将四边形![]() 的面积表示为关于
的面积表示为关于![]() 的表达式,进而可以求出最大值.
的表达式,进而可以求出最大值.
试题解析:(1)依题意,点 在椭圆
在椭圆![]() .
.
∵![]() ,
,
又∵![]() ,∴
,∴![]() .
.
∴椭圆![]() 的方程为
的方程为![]() .
.
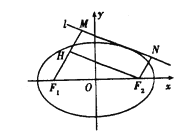
(2)将直线![]() 的方程
的方程![]() 代入椭圆
代入椭圆![]() 的方程
的方程![]() 中,得
中,得
![]() .
.
由直线![]() 与椭圆
与椭圆![]() 仅有一个公共点知,
仅有一个公共点知, ![]() ,
,
化简得: ![]() .
.
设![]() ,
,
∵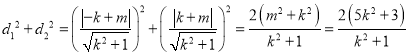 ,
,
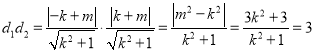 .
.
∴![]() ,
,
四边形![]() 的面积
的面积![]() ,
,
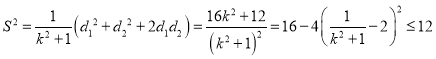 .
.
当且仅当![]() 时,
时, ![]() ,故
,故![]() .
.
所以四边形![]() 的面积
的面积![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】袋中装有偶数个球,其中红球、黑球各占一半,甲、乙、丙是三个空盒.每次从袋中任取两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都放入盒中,则( )
A. 乙盒中红球与丙盒中黑球一样多
B. 乙盒中黑球不多于丙盒中黑球
C. 乙盒中红球不多于丙盒中红球
D. 乙盒中黑球与丙盒中红球一样多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 在
在![]() 上的最小值;
上的最小值;
(2)对一切![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)探讨函数![]() 是否存在零点?若存在,求出函数
是否存在零点?若存在,求出函数![]() 的零点;若不存在,请说明理由.
的零点;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水泥厂销售工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示:
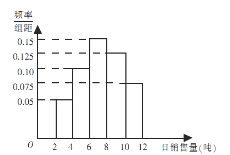
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求未来3天内,连续2天日销售量不低于8吨,另一天日销售量低于8吨的概率;
(2)用![]() 表示未来3天内日销售量不低于8吨的天数,求随机变量
表示未来3天内日销售量不低于8吨的天数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中放有的黑球和白球,其中黑球4个,白球5个.
(1)从盒中同时摸出两个球,求两球颜色恰好相同的概率.
(2)从盒中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
(3)从盒中不放回的每次摸一球,若取到白球则停止摸球,求取到第三次时停止摸球的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)是奇函数,且满足f(x)=f(x+3),f(-2)=-3.若数列{an}中,a1=-1,且前n项和Sn满足![]() =2×
=2×![]() +1,则f(a5)+f(a6)=________.
+1,则f(a5)+f(a6)=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com