
分析 由题意,$\left\{\begin{array}{l}{2p{x}_{0}=4}\\{{x}_{0}+\frac{p}{2}=\frac{5}{2}}\end{array}\right.$,消去x0,可得p2-5p+4=0,求出p,验证即可得出结论.
解答 解:由题意,$\left\{\begin{array}{l}{2p{x}_{0}=4}\\{{x}_{0}+\frac{p}{2}=\frac{5}{2}}\end{array}\right.$,消去x0,可得p2-5p+4=0,
∴p=1或4,
p=4时,x0=$\frac{1}{2}$<$\frac{p}{2}$,不符合题意.
故答案为1.
点评 本题主要考查了抛物线的定义和性质.考查了考生对抛物线定义的掌握和灵活应用,属于基础题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧(?q) | C. | (?p)∧(?q) | D. | (?p)∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3} | B. | {3,27,81} | C. | {1,3,9} | D. | {9,27} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
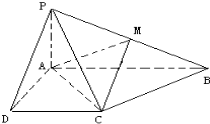 如图所示,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB∥CD,∠DAB=90°,PA⊥平面ABCD,且PA=CD=AD=$\frac{1}{2}$AB,M为PB的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB∥CD,∠DAB=90°,PA⊥平面ABCD,且PA=CD=AD=$\frac{1}{2}$AB,M为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com