
分析 (1)先求导,再判导数的符号.
(2)直接计算f(1)-1与f(2)-2、f(2)-2与f(3)-3,进行比较.比较大小可用做差比较法.归纳一般的结论,构造函数利用单调性进行证明.
解答 解:(Ⅰ)f′(x)=$\frac{a}{{a}^{2}-1}$(ax+a-x)lna,
若0<a<1,则$\frac{a}{{a}^{2}-1}$<0,lna<0,所以f′(x)>0;
若a>1,则$\frac{a}{{a}^{2}-1}$>0,lna>0,所以f′(x)>0,
因此,任意a>0且a≠1,都有f′(x)>0,f(x)在(-∞,+∞)上的单调递增.
(Ⅱ)直接计算知f(1)-1=0,f(2)-2=a+a-1-2,f(3)-3=a2+a-2-2,
根据基本不等式a+a-1-2>0,所以f(2)-2>f(1)-1,
又因为(a2+a-2-2)(a+a-1-2)=[(a+a-1)2-($\sqrt{a}$-$\sqrt{{a}^{-1}}$)2]=($\sqrt{a}$-$\sqrt{{a}^{-1}}$)2(a+a-1+1)=$\frac{1}{a}$(a-1)2(a+a-1+1)>0,
所以f(3)-3>f(2)-2.
假设?x>0,f(x+1)-(x+1)>f(x)-x.
记g(x)=[f(x+1)-(x+1)]-[f(x)-x]$\frac{a}{{a}^{2}-1}$[(ax+1-a-x-1)-((ax-a-x)]-1=$\frac{{a}^{x+1}+{a}^{-x}}{a+1}$-1,
g′(x)=$\frac{{a}^{x+1}+{a}^{-x}}{a+1}$lna,
与(Ⅰ)类似地讨论知,对?x>0和?a>0且a≠1都有g′(x)>0,g(x)在[0,+∞)上的单调递增,g(0)=0,
所以g(x)>g(0)=0,即?x>0,f(x+1)-(x+1)>f(x)-x.
点评 本题考查比较大小、归纳推理、函数单调性的证明及应用,综合性强,难度较大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于y轴对称 | B. | 关于原点对称 | ||
| C. | 关于直线x+y=0对称 | D. | 关于直线x-y=0对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
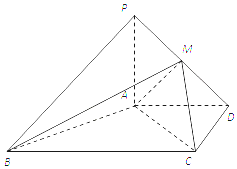 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f′(x)>0,g′(-x)>0 | B. | f′(x)>0,g′(-x)<0 | C. | f′(x)<0,g′(-x)>0 | D. | f′(x)<0,g′(-x)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | -2 | D. | -5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com