
分析 (Ⅰ)直接由基本初等函数的性质可得f(x)=log2|x|为偶函数;
(Ⅱ)①由(Ⅰ)知,$g(x)=m•{2^{{{log}_2}|x|}}+{x^2}={x^2}+m•|x|$,取绝对值,利用二次函数的对称轴$\frac{m}{2}≥-2$求实数m的取值范围;
②由$g(x)>\frac{x}{4}+\frac{1}{x}$,可得x2+m|x|$>\frac{x}{4}+\frac{1}{x}$.去绝对值得x2+mx$>\frac{x}{4}+\frac{1}{x}$,即4x3+(4m-1)x2-4>0.由m>$\frac{1}{4}$,可得函数F(x)=4x3+(4m-1)x2-4(1≤x≤2)为增函数,从而得到当$m>\frac{1}{4}$时,$g(x)>\frac{x}{4}+\frac{1}{x}$在x∈[1,2]上恒成立.
解答 解:(Ⅰ)由题意,f(x)=log2|x|,…(3分)
(Ⅱ)①由(Ⅰ)知,$g(x)=m•{2^{{{log}_2}|x|}}+{x^2}={x^2}+m•|x|$,
当x∈(-∞,-2),此时g(x)=x2-mx.
若函数g(x)在区间(-∞,-2)上是减函数,则$\frac{m}{2}≥-2$,∴m≥-4;…(6分)
②由$g(x)>\frac{x}{4}+\frac{1}{x}$,可得x2+m|x|$>\frac{x}{4}+\frac{1}{x}$.
若x∈[1,2],则x2+mx$>\frac{x}{4}+\frac{1}{x}$,
整理得,4x3+(4m-1)x2-4>0.…(8分)
因此问题转化为:
当$m>\frac{1}{4}$时,4x3+(4m-1)x2-4>0在x∈[1,2]上是否恒成立.…(9分)
令F(x)=4x3+(4m-1)x2-4(1≤x≤2),
当$m>\frac{1}{4}$时,则4m-1>0,可判断出函数F(x)在x∈[1,2]单调递增.
∴F(x)≥F(1)=4m-1>0.
因此,当$m>\frac{1}{4}$时,4x3+(4m-1)x2-4>0在x∈[1,2]上恒成立.
∴当$m>\frac{1}{4}$时,$g(x)>\frac{x}{4}+\frac{1}{x}$在x∈[1,2]上恒成立.…(12分)
点评 本题考查函数恒成立问题,考查对数函数的性质,考查数学转化思想方法,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{30}}}{10}$ | B. | $\frac{{\sqrt{30}}}{6}$ | C. | $\frac{{\sqrt{10}}}{6}$ | D. | $\frac{{2\sqrt{30}}}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4,D是AB中点,现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上一点,且∠BOC=90°,
如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4,D是AB中点,现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上一点,且∠BOC=90°,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{10}$+y2=1 | B. | $\frac{{x}^{2}}{19}$+$\frac{{y}^{2}}{10}$=1 | C. | $\frac{{x}^{2}}{27}$+$\frac{{y}^{2}}{18}$=1 | D. | $\frac{{x}^{2}}{18}$+$\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
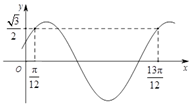 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )| A. | ω=2,$φ=\frac{π}{6}$ | B. | $ω=\frac{1}{2}$,$φ=\frac{π}{6}$ | C. | ω=2,$φ=\frac{π}{3}$ | D. | $ω=\frac{1}{2}$,$φ=\frac{π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com