
分析 (I)求出原函数的导函数利用导数求出f(x)在x=0处的切线方程,由切线过点(2,-1)可求a的值;
(Ⅱ)求出原函数的导函数,然后对a分类求解函数f(x)在(1,+∞)上的单调性;
(Ⅲ)由题意求得F(x)=xf(x)-x2=xex,求出函数F(x)的单调区间,可得在x=-1时,F(x)取得极小值和最小值.然后再构造辅助函数,借助于导数证明结论.
解答 (1)解:由f(x)=ex+ax,得f′(x)=ex+a,
f(0)=1,f′(0)=a+1,
∴f(x)在x=0处的切线为y=(a+1)x+1,
∵f(x)在x=0处的切线过点(2,-1),
∴-1=2(a+1)+1,解得a=-2;
(2)解:∵f′(x)=ex+a,
当a≥-e时,f′(x)=ex+a≥0,函数f(x)在(1,+∞)上单调递增;
当a<-e时,由f′(x)=ex+a=0,得ex=-a,x=ln(-a),
∴当x∈(1,ln(-a))时,f′(x)<0,f(x)单调递减;
当x∈(ln(-a),+∞)时,f′(x)>0,f(x)单调递增;
(3)证明:当a=1时,f(x)=ex+x,
F(x)=xf(x)-x2 =xex+x2-x2=xex,
F′(x)=ex+xex=ex(x+1),
由F′(x)=0,得x=-1,
∴当x∈(-∞,-1)时,F′(x)<0,F(x)为减函数;
当x∈(-1,+∞)时,F′(x)>0,F(x)为增函数.
在x=-1时,F(x)取得极小值和最小值.
又当x趋近于-∞时,F(x)负向趋近于0,且F(0)=0,
∴如果存在x1≠x2,使得F(x1)=F(x2),不失一般性令x1<x2,则x1<-1,-1<x2<0.
对于任意的x∈(-1,0),分别取两点-1-x、-1+x.
现在比较F(-1-x)和F(-1+x)的大小.
F(-1-x)-F(1+x)=(-1-x)e-1-x-(-1+x)e-1+x=$\frac{-[(1+x)+(1-x){e}^{2x}]}{{e}^{1+x}}$,
令g(x)=-(1+x)-(1-x)e2x,x∈(-1,0).
有g′(x)=-1+(2x-1)e2x,x∈(0,1).
当x=0时,g′(x)=0;
当x<0时,-1+(2x-1)e2x单调递间且小于0.
∴在(-1,0)上g(x)是单调减函数,且g(x)<g(0)=0,
有F(-1-x)-F(-1+x)<0,
即F(-1+x)>F(-1-x),
∵-1<-1-x<0,-1+x<-1,F(x)在(-∞,-1]上单调递减且F(-1+x)>F(-1-x),
在-1+x点的左侧必能找到一点x2,使得F(-1-x)=F(x2),x2<-1+x.
故(-1+x)+x2<(-1+x)+(-1-x)=-2
令-1+x=x1,
则为x1+x2<-2.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查了利用导数研究函数的单调性,训练了利用导数证明函数不等式,考查分析问题和解决问题的能力,属压轴题.


科目:高中数学 来源: 题型:解答题
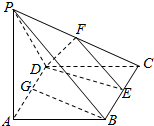 如图所示,在四棱柱P-ABCD中,底面ABCD是菱形,∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,
如图所示,在四棱柱P-ABCD中,底面ABCD是菱形,∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
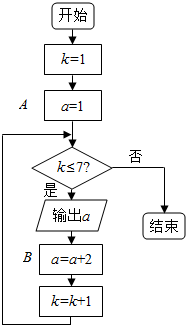 按图所示的程序框图操作:
按图所示的程序框图操作:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{6}}}{4}$ | B. | $-\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{6}}}{4}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2$\sqrt{3}$ | B. | -$\frac{2\sqrt{3}}{3}$ | C. | 0 | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=lnx2,g(x)=2lnx | B. | f(x)=x,g(x)=($\sqrt{x}$)2 | ||
| C. | f(x)=cosx•tanx,g(x)=sinx | D. | f(x)=x2,g(x)=$\sqrt{{x}^{4}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com