Question

在长方体ABCD-A₁B₁C₁D₁中，AB=BC=1，AA₁=2，E为BB₁中点．
（Ⅰ）证明：AC⊥D₁E；
（Ⅱ）求DE与平面AD₁E所成角的正弦值．

Answer 1

考点：直线与平面所成的角

专题：综合题,空间位置关系与距离,空间角

分析：（I）根据已知中长方体ABCD-A₁B₁C₁D₁中，AB=BC=1，AA₁=2，E是侧棱BB₁的中点，结合长方体的几何特征，我们可得D₁D⊥AC，BD⊥AC，结合线面垂直的判定定理即可得到AC⊥平面BB₁D₁D，即可得出结论；
（Ⅱ）建立空间直角坐标系，求出平面AD₁E的法向量，利用向量的夹角公式，即可求DE与平面AD₁E所成角的正弦值．

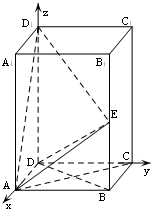
解答： （Ⅰ）证明：连接BD
∵ABCD-A₁B₁C₁D₁是长方体，
∴D₁D⊥平面ABCD，
又AC?平面ABCD
∴D₁D⊥AC…（1分）
在长方形ABCD中，AB=BC
∴BD⊥AC…（2分）
又BD∩D₁D=D
∴AC⊥平面BB₁D₁D，…（3分）      
而D₁E?平面BB₁D₁D
∴AC⊥D₁E…（4分）
（Ⅱ）解：如图建立空间直角坐标系D-xyz，则A（1，0，0），D₁（0，0，2），E（1，1，1），B（1，1，0），

AE

=(0，1，1)，

AD1

=(-1，0，2)，

DE

=(1，1，1)
设平面AD₁E的法向量为

n

=(x，y，z)，则

-x+2z=0 y+z=0

，
令z=1，则

n

=(2，-1，1)…（8分）
∴cos＜

n

，

DE

＞=

2-1+1

3 • 6

=

2

3

          …（10分）
∴DE与平面AD₁E所成角的正弦值为

2

3

…（12分）

点评：本题考查的知识点是直线与平面垂直的判定与性质，考查线面角，正确运用直线与平面垂直的判定与性质是关键．