
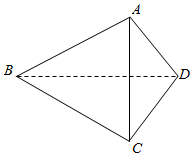
 如图所示的四面体ABCD中,AB⊥AD,CD⊥DB,BD=DC=5,AB=4.
如图所示的四面体ABCD中,AB⊥AD,CD⊥DB,BD=DC=5,AB=4.分析 (1)按照逆向思维,假设面ABD⊥面BCD,得出CD⊥AD,继而求解AC的值;
(2)由已知可得AD⊥面ABC,将待求体积进行转化:VA-BCD=VD-ABC,利用已知条件求解即可.
解答 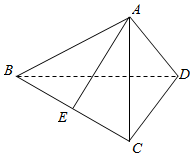 解:(1)若面ABD⊥面BCD,
解:(1)若面ABD⊥面BCD,
∵面ABD∩面BCD=BD,又CD⊥BD,则CD⊥面ABD,∴CD⊥AD.
由已知可得AD=3,则$AC=\sqrt{C{D}^{2}+A{D}^{2}}=\sqrt{34}$.
∴当AC的长为$\sqrt{34}$时,面ABD⊥面BCD;
(2)∵点D到面ABC的距离为3,且AD=3,∴AD⊥平面ABC,则AD⊥AC,
∴$AC=\sqrt{C{D}^{2}-A{D}^{2}}=4$,又CD⊥DB,BD=DC=5,
∴BC=5$\sqrt{2}$,取BC中点E,连接AE,则AE=$\sqrt{A{C}^{2}-(\frac{BC}{2})^{2}}$=$\frac{\sqrt{14}}{2}$.
∴${S}_{△ABC}=\frac{1}{2}BC•AE=\frac{5\sqrt{7}}{2}$.
∴${V}_{A-BCD}={V}_{D-ABC}=\frac{1}{3}{S}_{△ABC}•AD$=$\frac{1}{3}×\frac{5\sqrt{7}}{2}×3=\frac{5\sqrt{7}}{2}$.
点评 本题考查平面与平面垂直的判断,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
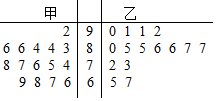 某农场用甲、乙两种不同的方式培育了一批甘蔗苗,培育一段时间后,同时随机抽取两种方式培育的甘蔗苗各15株,测量其高度,得到如图的茎叶图(单位:cm)
某农场用甲、乙两种不同的方式培育了一批甘蔗苗,培育一段时间后,同时随机抽取两种方式培育的甘蔗苗各15株,测量其高度,得到如图的茎叶图(单位:cm)| 甲方式 | 乙方式 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (1,+∞) | C. | (-∞,0) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 73 | 72 | 71 | 73 | 69 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-11,2) | B. | (-2,11) | C. | (11,-2) | D. | (2,-11) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com