设曲线y=f(x)与曲线y=x2+1关于y=x对称.则fA．B．C．D．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

19．设曲线y=f（x）与曲线y=x²+1（x＜0）关于y=x对称，则f（x）的定义域为（　　）

A．

（0，+∞）

B．

（1，+∞）

C．

（-∞，0）

D．

（-∞，1）

分析根据函数关于y=x对称，得到两个函数互为反函数，根据互为反函数的定义域和值域的关系，转化求函数y=x²+1（x＜0）的值域即可．

解答解：∵曲线y=f（x）与曲线y=x²+1（x＜0）关于y=x对称，
∴函数f（x）与y=x²+1（x＜0）互为反函数，
要求f（x）的定义域，即求函数y=x²+1（x＜0）的值域，
∵x＜0，∴y=x²+1＞1，即y=x²+1（x＜0）的值域为（1，+∞），
则函数f（x）的定义域为（1，+∞），
故选：B

点评本题主要考查反函数的性质，根据条件判断两个函数互为反函数，利用反函数的定义域和值域的关系是解决本题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

9．

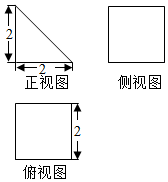如图是一个正方体被一个平面截去一部分后得到的几何体的三视图，则该几何体的体积是原正方体的体积的（　　）

A．

$\frac{3}{4}$

B．

$\frac{1}{4}$

C．

$\frac{1}{2}$

D．

$\frac{3}{8}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

10．在平行四边形ABCD中，AB=3，AD=2，∠BAD=60°，$\overrightarrow{DE}$=t$\overrightarrow{DC}$（0≤t≤1），且$\overrightarrow{AE}$•$\overrightarrow{BD}$=-1，则t=$\frac{1}{3}$．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

7．若$\overrightarrow{a}$和$\overrightarrow{b}$是两个互相垂直的单位向量，则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{5}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

14．

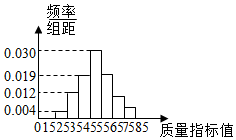针对当前市场的低迷，企业在不断开拓市场的同时，也在不断的加强产品质量的管理．我市某企业从生产的某种产品中抽取100件，测量这些产品的质量指标值，由测量结果得到如图所示的频率分布直方图，质量指标值落在区间[55，65），[65，75），[75，85]内的频率之比为4：2：1．
（1）求这些产品质量指标值落在区间[75，85]内的频率；
（2）用分层抽样的方法在区间[45，75）内抽取一个容量为6的样本，将该样本看成一个总体，从中任意抽取2件产品，求这2件产品都在区间[45，65）内的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．

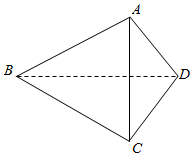如图所示的四面体ABCD中，AB⊥AD，CD⊥DB，BD=DC=5，AB=4．
（1）当AC的长为多少时，面ABD⊥面BCD；
（2）当点D到面ABC的距离为3时，求该四面体ABCD的体积．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

11．已知a＜0，则x₀满足关于x的方程ax=b的充要条件是（　　）

	A．	?x∈R，$\frac{1}{2}$ax²-bx≥$\frac{1}{2}$ax${\;}_{0}^{2}$-bx₀		B．	?x∈R，$\frac{1}{2}$ax²-bx≤$\frac{1}{2}$ax${\;}_{0}^{2}$-bx₀
	C．	?x∈R，$\frac{1}{2}$ax²-bx≥$\frac{1}{2}$ax${\;}_{0}^{2}$-bx₀		D．	?x∈R，$\frac{1}{2}$ax²-bx≤$\frac{1}{2}$ax${\;}_{0}^{2}$-bx₀