
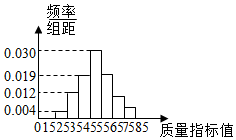
 针对当前市场的低迷,企业在不断开拓市场的同时,也在不断的加强产品质量的管理.我市某企业从生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.
针对当前市场的低迷,企业在不断开拓市场的同时,也在不断的加强产品质量的管理.我市某企业从生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.分析 (1)设这些产品质量指标值落在区间[75,85]内的频率为x,由题意得(0.004+0.012+0.019+0.030)×10+4x+2x+x=1,由此能求出这些产品质量指标值落在区间[75,85]内的频率.
(2)由频率分布直方图得区间[45,55)内有30件,区间[55,65)内有20件,区间[65,75)内有10件,用分层抽样的方法在区间[45,75)内抽取一个容量为6的样本,区间[45,55)内抽取3件,区间[55,65)内抽取2件,区间[65,75)内抽取1件,由此能求出这2件产品都在区间[45,65)内的概率.
解答 解:(1)设这些产品质量指标值落在区间[75,85]内的频率为x,
由题意得(0.004+0.012+0.019+0.030)×10+4x+2x+x=1,
解得x=0.05.
(2)由频率分布直方图得区间[45,55)内有0.03×10×100=30件,
区间[55,65)内有0.2×100=20件,
区间[65,75)内有0.1×100=10件,
用分层抽样的方法在区间[45,75)内抽取一个容量为6的样本,
则区间[45,55)内抽取6×$\frac{30}{30+20+10}$=3件,
区间[55,65)内抽取6×$\frac{20}{30+20+10}$=2件,
区间[65,75)内抽取6×$\frac{10}{30+20+10}$=1件,
将该样本看成一个总体,从中任意抽取2件产品,基本事件总数n=${C}_{6}^{2}$=15,
这2件产品都在区间[45,65)内包含的基本事件个数m=${C}_{5}^{2}$=10,
∴这2件产品都在区间[45,65)内的概率p=$\frac{m}{n}$=$\frac{10}{15}$=$\frac{2}{3}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是中档题,解题时要认真审题,注意分层抽样的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{14}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{13}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (1,+∞) | C. | (-∞,0) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$+$\sqrt{3}$ | D. | $\sqrt{3}$-$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com