
| A. | $\frac{5}{14}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{13}$ | D. | $\frac{5}{9}$ |
分析 求得椭圆的a,b,c,运用椭圆的定义和三角形的中位线定理,可得PF2⊥x轴,|PF2|=$\frac{5}{3}$,|PF1|=$\frac{13}{3}$,计算即可所求值.
解答 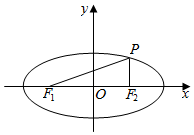 解:椭圆$\frac{x^2}{9}+\frac{y^2}{5}$=1的a=3,b=$\sqrt{5}$,c=$\sqrt{{a}^{2}-{b}^{2}}$=2,
解:椭圆$\frac{x^2}{9}+\frac{y^2}{5}$=1的a=3,b=$\sqrt{5}$,c=$\sqrt{{a}^{2}-{b}^{2}}$=2,
由椭圆的定义可得|PF1|+|PF2|=2a=6,
由中位线定理可得PF2⊥x轴,
令x=2,可得y=±$\sqrt{5}$•$\sqrt{1-\frac{4}{9}}$=±$\frac{5}{3}$,
即有|PF2|=$\frac{5}{3}$,|PF1|=6-$\frac{5}{3}$=$\frac{13}{3}$,
则$\frac{{|{P{F_2}}|}}{{|{P{F_1}}|}}$=$\frac{5}{13}$.
故选:C.
点评 本题考查椭圆的定义,三角形的中位线定理的运用,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{kπ-\frac{π}{3},kπ+\frac{π}{6}}](k∈Z)$ | B. | [kπ,kπ$+\frac{π}{2}$](k∈Z) | C. | $[{kπ-\frac{π}{2},kπ}](k∈Z)$ | D. | $[{kπ+\frac{π}{6},kπ+\frac{2π}{3}}](k∈Z)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{4\sqrt{17}}}{17}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
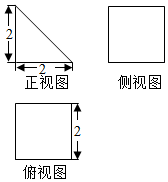 如图是一个正方体被一个平面截去一部分后得到的几何体的三视图,则该几何体的体积是原正方体的体积的( )
如图是一个正方体被一个平面截去一部分后得到的几何体的三视图,则该几何体的体积是原正方体的体积的( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
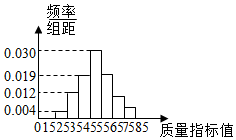 针对当前市场的低迷,企业在不断开拓市场的同时,也在不断的加强产品质量的管理.我市某企业从生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.
针对当前市场的低迷,企业在不断开拓市场的同时,也在不断的加强产品质量的管理.我市某企业从生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com