
分析 (I)利用正弦定理将边化角,根据sinA=sin(B+C)进行化简,即可得出解出cosB,得到B的值;
(II)分别在△ABC和△ABM中使用余弦定理,联立方程组解出a.
解答 解:(I)∵2bsin(C+$\frac{π}{6}$)=a+c,
∴b($\sqrt{3}$sinC+cosC)=a+c,即$\sqrt{3}$bsinC+bcosC=a+c,
∴$\sqrt{3}$sinBsinC+sinBcosC=sinA+sinC=sin(B+C)+sinC=sinBcosC+cosBsinC+sinC
∴$\sqrt{3}$sinBsinC=cosBsinC+sinC,
∵sinC≠0,
∴$\sqrt{3}$sinB=cosB+1,
两边平方得:3sin2B=cos2B+1+2cosB,
∴2cos2B+cosB-1=0,
解得cosB=$\frac{1}{2}$或-1,
∵0<B<π,
∴B=$\frac{π}{3}$.
(II)BM=CM=$\frac{a}{2}$,
在△ABC中,由余弦定理得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}=\frac{1}{2}$,即$\frac{{a}^{2}+{c}^{2}-4}{2ac}=\frac{1}{2}$,∴a2+c2-4=ac,
在△ABM中,由余弦定理得:cosB=$\frac{B{M}^{2}+A{B}^{2}-A{M}^{2}}{2BM•AB}$=$\frac{1}{2}$,即$\frac{\frac{{a}^{2}}{4}+{c}^{2}-4}{ac}=\frac{1}{2}$,∴$\frac{{a}^{2}}{4}+{c}^{2}-4=\frac{1}{2}ac$.
∴联立方程组$\left\{\begin{array}{l}{{a}^{2}+{c}^{2}-4=ac}\\{\frac{{a}^{2}}{4}+{c}^{2}-4=\frac{ac}{2}}\end{array}\right.$,解得a=$\frac{4\sqrt{7}}{7}$.
点评 本题考查了正弦定理,余弦定理,三角函数的恒等变换,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $[{kπ-\frac{π}{3},kπ+\frac{π}{6}}](k∈Z)$ | B. | [kπ,kπ$+\frac{π}{2}$](k∈Z) | C. | $[{kπ-\frac{π}{2},kπ}](k∈Z)$ | D. | $[{kπ+\frac{π}{6},kπ+\frac{2π}{3}}](k∈Z)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
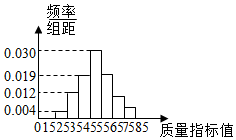 针对当前市场的低迷,企业在不断开拓市场的同时,也在不断的加强产品质量的管理.我市某企业从生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.
针对当前市场的低迷,企业在不断开拓市场的同时,也在不断的加强产品质量的管理.我市某企业从生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com