
【题目】已知定义在实数集![]() 上的偶函数
上的偶函数![]() 和奇函数
和奇函数![]() 满足
满足![]() .
.
(1)求![]() 与
与![]() 的解析式;
的解析式;
(2)若定义在实数集![]() 上的以2为最小正周期的周期函数
上的以2为最小正周期的周期函数![]() ,当
,当![]() 时,
时,![]() ,试求
,试求![]() 在闭区间
在闭区间![]() 上的表达式,并证明
上的表达式,并证明![]() 在闭区间
在闭区间![]() 上单调递减;
上单调递减;
(3)设![]() (其中
(其中![]() 为常数),若
为常数),若![]() 对于
对于![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() (2)
(2)![]() ;证明见解析(3)
;证明见解析(3)![]()
【解析】
(1)根据奇函数与偶函数定义,可分别代入得关于![]() 与
与![]() 的方程组,解方程组即可求得
的方程组,解方程组即可求得![]() 与
与![]() 的解析式;
的解析式;
(2)由![]() 为以2为最小正周期的周期函数,所以当
为以2为最小正周期的周期函数,所以当![]() 时
时![]() ,即可根据
,即可根据![]() 求得求
求得求![]() 在闭区间
在闭区间![]() 上的表达式.根据函数单调性的定义,任取
上的表达式.根据函数单调性的定义,任取![]() ,即可通过作差法证明函数的单调性.
,即可通过作差法证明函数的单调性.
(3)利用换元法,令![]() ,由
,由![]() 可求得
可求得![]() 的取值范围.则
的取值范围.则![]() .由
.由![]() 可知当
可知当![]() 时满足
时满足![]() ,因而可知
,因而可知![]() 恒成立.分离参数
恒成立.分离参数![]() 可知
可知![]() ,结合基本不等式即可求得
,结合基本不等式即可求得![]() 的取值范围.
的取值范围.
(1)由![]() ①,
①,
因为![]() 是偶函数,
是偶函数,![]() 是奇函数
是奇函数
所以有![]() ,即
,即![]() ②
②
∵![]() ,
,![]() 定义在实数集
定义在实数集![]() 上
上
由①和②解得![]() ,
,![]()
(2)![]() 是
是![]() 上以2为正周期的周期函数
上以2为正周期的周期函数
所以当![]() 时,
时,![]()
![]()
![]()
即![]() 在闭区间
在闭区间![]() 上的表达式为
上的表达式为![]()
下面证明![]() 在闭区间
在闭区间![]() 上递减:
上递减:
![]() ,当且仅当
,当且仅当![]()
即![]() 时等号成立.对于任意
时等号成立.对于任意![]()
![]()
![]()
![]()
因为![]() ,所以
,所以![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
从而![]() ,所以当
,所以当![]() 时,
时,![]() 递减
递减
(3)∵![]() 在
在![]() 单调递增
单调递增
∴![]()
∴![]()
![]() 对于
对于![]() 恒成立
恒成立
∴![]() 对于
对于![]() 恒成立
恒成立
令![]() ,则
,则![]()
当且仅当![]() 时,等号成立,且
时,等号成立,且![]()
所以在区间![]() 上
上![]() 单调递减
单调递减
∴![]()
∴![]() 为
为![]() 的取值范围
的取值范围


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,且经过点
的中心在坐标原点,且经过点![]() ,它的一个焦点与抛物线E:
,它的一个焦点与抛物线E:![]() 的焦点重合,斜率为k的直线l交抛物线E于A、B两点,交椭圆
的焦点重合,斜率为k的直线l交抛物线E于A、B两点,交椭圆![]() 于C、D两点.
于C、D两点.
(1)求椭圆![]() 的方程;
的方程;
(2)直线l经过点![]() ,设点
,设点![]() ,且
,且![]() 的面积为
的面积为![]() ,求k的值;
,求k的值;
(3)若直线l过点![]() ,设直线
,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差数列,求直线l的方程.
成等差数列,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() ,
,![]() ,
,![]() 满足:对任意的
满足:对任意的![]() ,都有
,都有![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() .记
.记![]() =
=![]() (
(![]() 表示
表示![]() 个实数
个实数![]() ,
,![]() ,
,![]() 中的最大值).
中的最大值).
(1)若![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,求
,求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若![]() =
=,
![]() =
=![]() ,求满足
,求满足![]() =
=![]() 的
的![]() 的所有值;
的所有值;
(3)设![]() ,
,![]() ,
,![]() 是非零整数,且
是非零整数,且![]() ,
,![]() ,
,![]() 互不相等,证明:存在正整数
互不相等,证明:存在正整数![]() ,使得数列
,使得数列![]() ,
,![]() ,
,![]() 中有且只有一个数列自第
中有且只有一个数列自第![]() 项起各项均为
项起各项均为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在实数集![]() 上的偶函数
上的偶函数![]() 和奇函数
和奇函数![]() 满足
满足![]() .
.
(1)求![]() 与
与![]() 的解析式;
的解析式;
(2)若定义在实数集![]() 上的以2为最小正周期的周期函数
上的以2为最小正周期的周期函数![]() ,当
,当![]() 时,
时,![]() ,试求
,试求![]() 在闭区间
在闭区间![]() 上的表达式,并证明
上的表达式,并证明![]() 在闭区间
在闭区间![]() 上单调递减;
上单调递减;
(3)设![]() (其中
(其中![]() 为常数),若
为常数),若![]() 对于
对于![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 和
和![]() 是双曲线
是双曲线![]() 上的两点,线段
上的两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 不经过坐标原点
不经过坐标原点![]() .
.
(1)若直线![]() 和直线
和直线![]() 的斜率都存在且分别为
的斜率都存在且分别为![]() 和
和![]() ,求证:
,求证:![]() ;
;
(2)若双曲线的焦点分别为![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求由四点
,求由四点![]() 、
、![]() 、
、![]() 、
、![]() 所围成四边形
所围成四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
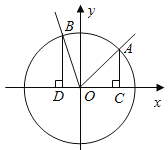
【题目】(本小题满分13分)如图,在直角坐标系![]() 中,角
中,角![]() 的顶点是原点,始边与
的顶点是原点,始边与![]() 轴正半轴重合.终边交单位圆于点
轴正半轴重合.终边交单位圆于点![]() ,且
,且![]() ,将角
,将角![]() 的终边按逆时针方向旋转
的终边按逆时针方向旋转![]() ,交单位圆于点
,交单位圆于点![]() ,记
,记![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)分别过![]() 作
作![]() 轴的垂线,垂足依次为
轴的垂线,垂足依次为![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求角
,求角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家号召,打赢脱贫致富攻坚战,武汉大学团队带领湖北省大悟县新城镇熊湾村村民建立有机、健康、高端、绿色的蔬菜基地,并策划“生产、运输、销售”一体化的直销供应模式,据统计,当地村民两年时间成功脱贫.蔬菜种植基地将采摘的有机蔬菜以每份三斤称重并保鲜分装,以每份10元的价格销售到生鲜超市,每份15元的价格卖给顾客,如果当天前8小时卖不完,则超市通过促销以每份5元的价格卖给顾客(根据经验,当天能够把剩余的有机蔬菜都低价处理完毕,且处理完毕后,当天不再进货).该生鲜超市统计了100天有机蔬菜在每天的前8小时内的销售量(单位:份),制成如下表格(注:![]() ,且
,且![]() ).若以100天记录的频率作为每日前8小时销售量发生的概率,该生鲜超市当天销售有机蔬菜利润的期望值为决策依据,若购进17份比购进18份的利润的期望值大,则x的最小值是________.
).若以100天记录的频率作为每日前8小时销售量发生的概率,该生鲜超市当天销售有机蔬菜利润的期望值为决策依据,若购进17份比购进18份的利润的期望值大,则x的最小值是________.
前8小时内销售量 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
频数 | 10 | x | 16 | 16 | 15 | 13 | y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com