
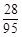 ;(2)详见解析.
;(2)详见解析.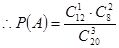 ,计算得到结果;(2)每位教师选择高一年级的概率均为
,计算得到结果;(2)每位教师选择高一年级的概率均为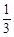 ,并且相互独立,X的所有取值为0,1,2,3,4.
,并且相互独立,X的所有取值为0,1,2,3,4. ,
,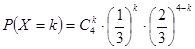 ,
,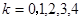 ,然后列出随机变量X的概率分布列,利用
,然后列出随机变量X的概率分布列,利用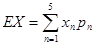 ,或是利用二项分布的期望公式
,或是利用二项分布的期望公式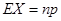 ,得出结果.随机变量的概率,分布列,期望还是高考的重点内容,属于基础题型,
,得出结果.随机变量的概率,分布列,期望还是高考的重点内容,属于基础题型,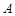 ,
,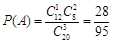 .
.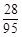 . 4分
. 4分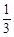 , 7分
, 7分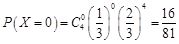 ;
;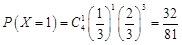
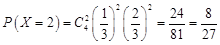 ;
;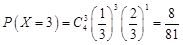 ;
;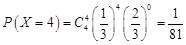 .
.| X | 0 | 1 | 2 | 3 | 4 |
| P | 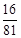 | 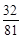 | 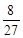 | 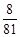 | 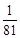 |
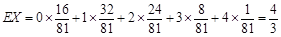 . 13分
. 13分

科目:高中数学 来源:不详 题型:解答题
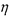 的方差是多少?
的方差是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
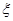 为四个小球得分总和.
为四个小球得分总和.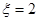 时的概率;
时的概率;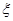 的概率分布及数学期望.
的概率分布及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响. ,求走公路②堵车的概率;
,求走公路②堵车的概率;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com