
| A. | [1,+∞) | B. | [-2,1] | C. | (-∞,-2]∪[1,+∞) | D. | (-∞,-2] |
分析 由当x>0时,x2+mx+1≥0恒成立,得到m≥-(x+$\frac{1}{x}$),利用基本不等式即可求出m的范围,再根据关于t的不等式t2+2t+m≤0有解,则△=4-4m≥0,最后求其交集即可.
解答 解:∵当x>0时,x2+mx+1≥0恒成立,
∴m≥-(x+$\frac{1}{x}$),
∵x+$\frac{1}{x}$≥2$\sqrt{x•\frac{1}{x}}$=2,当且仅当x=1时取等号,
∴m≥-2,
∵关于t的不等式t2+2t+m≤0有解,
∴△=4-4m≥0,
∴m≤1,
∴实数m的取值范围是[-2,1],
故选:B.
点评 本题考查的知识点是二次函数的图象和性质以及基本不等式,熟练掌握二次函数的图象和性质是解答的关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
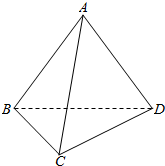
| A. | -2 | B. | 2 | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com