
【题目】已知函数f(x)=x2+a(x+lnx),a∈R. (Ⅰ)若当a=﹣1时,求f(x)的单调区间;
(Ⅱ)若f(x)> ![]() (e+1)a,求a的取值范围.
(e+1)a,求a的取值范围.
【答案】解:(Ⅰ)由题意得x∈(0,+∞); 当a=﹣1时,f(x)=x2﹣x﹣lnx, ![]() =
= ![]() ;
;
∴x∈(0,1)时,f′(x)<0,x∈(1,+∞)时,f′(x)>0;
∴f(x)的单调减区间是(0,1),单调增区间是[1,+∞);
(Ⅱ)①当a=0时,f(x)=x2>0,显然符合题意;
②当a>0时,当 ![]() 时;
时;
f(x)<1+a+alnx ![]() ,不符合题意;
,不符合题意;
③当a<0时,则 ![]() ;
;
对于2x2+ax+a=0,△=a2﹣8a>0;
∴该方程有两个不同实根,且一正一负,即存在x0∈(0,+∞),使得 ![]() ;
;
即f′(x0)=0;
∴0<x<x0时,f′(x)<0,x>x0时,f′(x)>0;
∴f(x)min=f(x0)= ![]() =
= ![]() =
= ![]() ;
;
∵ ![]() ,∴x0+2lnx0﹣(e+2)<0;
,∴x0+2lnx0﹣(e+2)<0;
∴0<x0<e;
由 ![]() 得,
得, ![]() ;
;
设y= ![]() ,y′=
,y′= 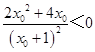 ;
;
∴函数 ![]() 在(0,e)上单调递减;
在(0,e)上单调递减;
∴ 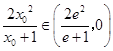 ;
;
综上所述,实数a的取值范围 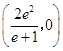
【解析】(Ⅰ)a=﹣1时,求出f(x)=x2﹣x﹣lnx,通过求导,根据导数符号即可判断出f(x)的单调区间;(Ⅱ)讨论a的取值:a=0时,容易得出满足题意;a>0时,会发现函数x2+ax在(0,+∞)上单调递增,让 ![]() <1,便得到f(x)<1+a+alnx
<1,便得到f(x)<1+a+alnx ![]() ,从而这种情况不存在;当a<0时,通过求导,容易判断出,存在x0∈(0,+∞),使f′(x0)=0,从而判断出f(x)的最小值f(x0),再由条件f(x)
,从而这种情况不存在;当a<0时,通过求导,容易判断出,存在x0∈(0,+∞),使f′(x0)=0,从而判断出f(x)的最小值f(x0),再由条件f(x) ![]() 便可得到x0∈(0,e),并根据f′(x0)=0,可求出
便可得到x0∈(0,e),并根据f′(x0)=0,可求出 ![]() ,从而求出a的取值范围.
,从而求出a的取值范围.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).


科目:高中数学 来源: 题型:
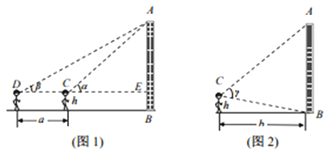
【题目】某校高一数学研究小组测量学校的一座教学楼AB的高度![]() 已知测角仪器距离地面的高度为h米,现有两种测量方法:
已知测角仪器距离地面的高度为h米,现有两种测量方法:
方法![]() 如图
如图![]() 用测角仪器,对准教学楼的顶部A,计算并记录仰角
用测角仪器,对准教学楼的顶部A,计算并记录仰角![]() ;
;![]() 后退a米,重复
后退a米,重复![]() 中的操作,计算并记录仰角
中的操作,计算并记录仰角![]() .
.
方法![]() 如图
如图![]() 用测角仪器,对准教学楼的顶部A底部B,测出教学楼的视角
用测角仪器,对准教学楼的顶部A底部B,测出教学楼的视角![]() ,测试点与教学楼的水平距离b米.
,测试点与教学楼的水平距离b米.
请你回答下列问题:
![]() 用数据
用数据![]() ,
,![]() ,a,h表示出教学楼AB的高度;
,a,h表示出教学楼AB的高度;
![]() 按照方法II,用数据
按照方法II,用数据![]() ,b,h表示出教学楼AB的高度.
,b,h表示出教学楼AB的高度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为![]() 的圆,满足下列条件:圆心
的圆,满足下列条件:圆心![]() 位于
位于![]() 轴正半轴上,与直线
轴正半轴上,与直线![]() 相切,且被
相切,且被![]() 轴截得的弦长为
轴截得的弦长为![]() ,圆
,圆![]() 的面积小于13.
的面积小于13.
(1)求圆![]() 的标准方程;
的标准方程;
(2)若点![]() ,点
,点![]() 是圆
是圆![]() 上一点,点
上一点,点![]() 是
是![]() 的重心,求点
的重心,求点![]() 的轨迹方程;
的轨迹方程;
(3)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,以
,以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() .是否存在这样的直线
.是否存在这样的直线![]() ,使得直线
,使得直线![]() 与
与![]() 恰好平行?如果存在,求出
恰好平行?如果存在,求出![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,直线l的参数方程 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为p2cos2θ+p2sinθ﹣2psinθ﹣3=0
(t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为p2cos2θ+p2sinθ﹣2psinθ﹣3=0
(1)求直线l的极坐标方程;
(2)若直线l与曲线C相交于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何学是美籍法国数学家伯努瓦![]() 曼德尔布罗特(
曼德尔布罗特(![]()
![]()
![]()
![]() )在20世纪70年代创立的一门新学科,它的创立为解决传统众多领域的难题提供了全新的思路.下图是按照分型的规律生长成的一个树形图,则第10行的空心圆的个数是__________.
)在20世纪70年代创立的一门新学科,它的创立为解决传统众多领域的难题提供了全新的思路.下图是按照分型的规律生长成的一个树形图,则第10行的空心圆的个数是__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() =(2﹣sin(2x+
=(2﹣sin(2x+![]() ),﹣2),
),﹣2),![]() =(1,sin2x),f(x)=
=(1,sin2x),f(x)=![]()
![]() , (x∈[0,
, (x∈[0,![]() ])
])
(1)求函数f(x)的值域;
(2)设△ABC的内角A,B,C的对边长分别为a,b,c,若f(![]() )=1,b=1,c=
)=1,b=1,c=![]() , 求a的值.
, 求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com