
【题目】已知![]() =(2﹣sin(2x+
=(2﹣sin(2x+![]() ),﹣2),
),﹣2),![]() =(1,sin2x),f(x)=
=(1,sin2x),f(x)=![]()
![]() , (x∈[0,
, (x∈[0,![]() ])
])
(1)求函数f(x)的值域;
(2)设△ABC的内角A,B,C的对边长分别为a,b,c,若f(![]() )=1,b=1,c=
)=1,b=1,c=![]() , 求a的值.
, 求a的值.
【答案】解:(1)f(x)=![]()
![]() =2﹣sin(2x+
=2﹣sin(2x+![]() )﹣2sin2x=2﹣(sin2xcos
)﹣2sin2x=2﹣(sin2xcos![]() +cos2xsin
+cos2xsin![]() )﹣(1﹣cos2x)=
)﹣(1﹣cos2x)=![]() cos2x﹣
cos2x﹣![]() sin2x+1=cos(2x+
sin2x+1=cos(2x+![]() )+1.
)+1.
∵x∈[0,![]() ],∴2x+
],∴2x+![]() ∈[
∈[![]() ,
,![]() ],∴﹣1≤cos(2x+
],∴﹣1≤cos(2x+![]() )≤
)≤![]() ,从而有0≤f(x)≤
,从而有0≤f(x)≤![]() ,
,
所以函数f(x)的值域为[0,![]() ].
].
(2)由f(![]() )=1,得cos(B+
)=1,得cos(B+![]() )=0,又因为0<B<π,所以
)=0,又因为0<B<π,所以![]() <B+
<B+![]()
![]()
![]() ,
,
从而B+![]() =
=![]() ,即B=
,即B=![]() .
.
因为b=1,c=![]() ,所以由正弦定理
,所以由正弦定理![]() 得sinC=
得sinC=![]() =
=![]() ,
,
故C=![]() 或
或![]() ,
,
当C=![]() 时,A=
时,A=![]() ,从而a=
,从而a=![]() =2,
=2,
当C=![]() 时,A=
时,A=![]() ,又B=
,又B=![]() ,从而a=b=1
,从而a=b=1
综上a的值为1或2
【解析】(1)利用平面向量数量积的运算及三角函数恒等变换的应用化简可得解析式f(x)=cos(2x+![]() )+1,由余弦函数的有界性即可求值域.
)+1,由余弦函数的有界性即可求值域.
(2)由f(![]() )=1,得cos(B+
)=1,得cos(B+![]() )=0,又结合范围0<B<π,即可解得B的值,由正弦定理可求sinC,解得C,解得A,即可解得a的值.
)=0,又结合范围0<B<π,即可解得B的值,由正弦定理可求sinC,解得C,解得A,即可解得a的值.
【考点精析】掌握两角和与差的正弦公式和正弦定理的定义是解答本题的根本,需要知道两角和与差的正弦公式:![]() ;正弦定理:
;正弦定理:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+a(x+lnx),a∈R. (Ⅰ)若当a=﹣1时,求f(x)的单调区间;
(Ⅱ)若f(x)> ![]() (e+1)a,求a的取值范围.
(e+1)a,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某中学为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识的竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐、规定:每场知识竞赛前三名的得分都分别为![]() (
(![]() ,且
,且![]() );选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
);选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
A. 每场比赛第一名得分![]() 为4 B. 甲可能有一场比赛获得第二名
为4 B. 甲可能有一场比赛获得第二名
C. 乙有四场比赛获得第三名 D. 丙可能有一场比赛获得第一名
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,A={y|y=2x+1},B={x|lnx<0},则(UA)∩B=( )
A.?
B.{x|![]() <x≤1}
<x≤1}
C.{x|x<1}
D.{x|0<x<1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 及圆
及圆![]() .
.
(1)若直线![]() 过点
过点![]() 且与圆心
且与圆心![]() 的距离为1,求直线
的距离为1,求直线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,当
两点,当![]() 时,求以线段
时,求以线段![]() 为直径的圆
为直径的圆![]() 的方程;
的方程;
(3)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,是否存在实数
两点,是否存在实数![]() ,使得过点
,使得过点![]() 的直线
的直线![]() 垂直平分弦
垂直平分弦![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 且a2=8,S4=40.数列{bn}的前n项和为Tn , 且Tn﹣2bn+3=0,n∈N* .
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=![]() , 求数列{cn}的前n项和Pn .
, 求数列{cn}的前n项和Pn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为数列{an}的前n项和,满足Sn=2an-2 (n∈N*)
(1)求![]() 的值,并由此猜想数列{an}的通项公式an;
的值,并由此猜想数列{an}的通项公式an;
(2)用数学归纳法证明(Ⅰ)中的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin(ωx+φ)(ω>0,﹣
sin(ωx+φ)(ω>0,﹣ ![]() ≤φ<
≤φ< ![]() )的图象关于直线x=
)的图象关于直线x= ![]() 对称,且图象上相邻两个最高点的距离为π.
对称,且图象上相邻两个最高点的距离为π.
(1)求ω和φ的值;
(2)若f( ![]() )=
)= ![]() (
( ![]() <α<
<α< ![]() ),求cos(α+
),求cos(α+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆C: ![]() (a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限.
(a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限. 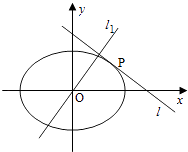
(1)已知直线l的斜率为k,用a,b,k表示点P的坐标;
(2)若过原点O的直线l1与l垂直,证明:点P到直线l1的距离的最大值为a﹣b.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com