
【题目】如图,设椭圆C: ![]() (a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限.
(a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限. 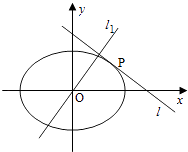
(1)已知直线l的斜率为k,用a,b,k表示点P的坐标;
(2)若过原点O的直线l1与l垂直,证明:点P到直线l1的距离的最大值为a﹣b.
【答案】
(1)解:设直线l的方程为y=kx+m(k<0),由 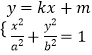 ,消去y得
,消去y得
(b2+a2k2)x2+2a2kmx+a2m2﹣a2b2=0.
由于直线l与椭圆C只有一个公共点P,故△=0,即b2﹣m2+a2k2=0,
此时点P的横坐标为﹣ ![]() ,代入y=kx+m得
,代入y=kx+m得
点P的纵坐标为﹣k ![]() +m=
+m= ![]() ,
,
∴点P的坐标为(﹣ ![]() ,
, ![]() ),
),
又点P在第一象限,故m>0,
故m= ![]() ,
,
故点P的坐标为P( ![]() ,
, ![]() ).
).
(2)解:由于直线l1过原点O且与直线l垂直,故直线l1的方程为x+ky=0,所以点P到直线l1的距离
d= 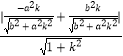 ,
,
整理得:d= 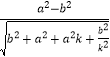 ,
,
因为a2k2+ ![]() ≥2ab,所以
≥2ab,所以 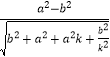 ≤
≤ ![]() =a﹣b,当且仅当k2=
=a﹣b,当且仅当k2= ![]() 时等号成立.
时等号成立.
所以,点P到直线l1的距离的最大值为a﹣b.

【解析】(1)设直线l的方程为y=kx+m(k<0),由 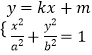 ,消去y得(b2+a2k2)x2+2a2kmx+a2m2﹣a2b2=0,利用△=0,可求得在第一象限中点P的坐标;(2)由于直线l1过原点O且与直线l垂直,设直线l1的方程为x+ky=0,利用点到直线间的距离公式,可求得点P到直线l1的距离d=
,消去y得(b2+a2k2)x2+2a2kmx+a2m2﹣a2b2=0,利用△=0,可求得在第一象限中点P的坐标;(2)由于直线l1过原点O且与直线l垂直,设直线l1的方程为x+ky=0,利用点到直线间的距离公式,可求得点P到直线l1的距离d= 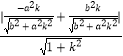 ,整理即可证得点P到直线l1的距离的最大值为a﹣b.
,整理即可证得点P到直线l1的距离的最大值为a﹣b.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() =(2﹣sin(2x+
=(2﹣sin(2x+![]() ),﹣2),
),﹣2),![]() =(1,sin2x),f(x)=
=(1,sin2x),f(x)=![]()
![]() , (x∈[0,
, (x∈[0,![]() ])
])
(1)求函数f(x)的值域;
(2)设△ABC的内角A,B,C的对边长分别为a,b,c,若f(![]() )=1,b=1,c=
)=1,b=1,c=![]() , 求a的值.
, 求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ae2x﹣be﹣2x﹣cx(a,b,c∈R)的导函数f′(x)为偶函数,且曲线y=f(x)在点(0,f(0))处的切线的斜率为4﹣c.
(1)确定a,b的值;
(2)若c=3,判断f(x)的单调性;
(3)若f(x)有极值,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
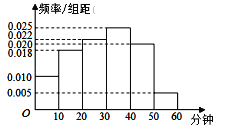
【题目】银川一中为研究学生的身体素质与课外体育锻炼时间的关系,抽取在校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集的数据分成![]() ,
,![]() 六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
课外体育不达标 | 课外体育达标 | 合计 | |
男 |
| ||
女 |
| ||
合计 |
(1)请根据直方图中的数据填写下面的![]() 列联表,并通过计算判断是否能在犯错误的概率不超过
列联表,并通过计算判断是否能在犯错误的概率不超过![]() 的前提下认为“课外体育达标”与性别有关?
的前提下认为“课外体育达标”与性别有关?
(2)在![]() 这两组中采取分层抽样,抽取6人,再从这6名学生中随机抽取2人参加体育知识问卷调查,求这2人中一人来自“课外体育达标”和一人来自“课外体育不达标”的概率.
这两组中采取分层抽样,抽取6人,再从这6名学生中随机抽取2人参加体育知识问卷调查,求这2人中一人来自“课外体育达标”和一人来自“课外体育不达标”的概率.
附参考公式与:![]()
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在其定义域内存在实数
,若在其定义域内存在实数![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 有“※点”
有“※点”![]() 。
。
(1)判断函数![]() 在
在![]() 上是否有“※点”。并说明理由;
上是否有“※点”。并说明理由;
(2)若函数![]() 在
在![]() 上有“※点”,求正实数a的取值范围。
上有“※点”,求正实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问100名性别不同的高二学生是否爱吃零食,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 10 | 40 | 50 |
不爱好 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
附表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
其中![]()
则下列结论正确的是( )
A. 在犯错误的概率不超过0.05的前提下,认为“是否爱吃零食与性别有关”
B. 在犯错误的概率不超过0.05的前提下,认为“是否爱吃零食与性别无关”
C. 在犯错误的概率不超过0.025的前提下,认为“是否爱吃零食与性别有关”
D. 在犯错误的概率不超过0.025的前提下,认为“是否爱吃零食与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列五个结论:
![]() 集合
集合![]() 2,3,4,5,
2,3,4,5,![]() ,集合
,集合![]() ,若f:
,若f:![]() ,则对应关系f是从集合A到集合B的映射;
,则对应关系f是从集合A到集合B的映射;
![]() 函数
函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域也是
的定义域也是![]() ;
;
![]() 存在实数
存在实数![]() ,使得
,使得![]() 成立;
成立;
![]() 是函数
是函数![]() 的对称轴方程;
的对称轴方程;
![]() 曲线
曲线![]() 和直线
和直线![]() 的公共点个数为m,则m不可能为1;
的公共点个数为m,则m不可能为1;
其中正确的有______![]() 写出所有正确的序号
写出所有正确的序号![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com