
设函数 ,其中
,其中
(1)求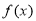 在的单调区间;
在的单调区间;
(2)当 时,求
时,求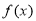 最小值及取得时的
最小值及取得时的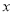 的值.
的值.
(1) 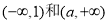 为
为 单调递增区间,
单调递增区间, 为
为 单调递减区间;
单调递减区间;
(2)当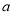 ≥3时,当
≥3时,当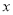 =3时,
=3时,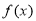 取最小值
取最小值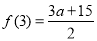 ,当
,当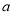 <3时,当
<3时,当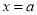 时,
时,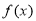 取最小值
取最小值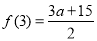
【解析】
试题分析:(1)先求出的导函数,由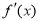 >0解出的区间即为
>0解出的区间即为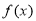 增区间,由
增区间,由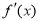 <0解出的区间即为
<0解出的区间即为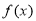 减区间; (2)将
减区间; (2)将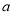 分成大于等于3与小于3两类,当
分成大于等于3与小于3两类,当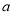 大于等于3时,由(1)知
大于等于3时,由(1)知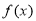 在[1,3]是单调递减函数,利用函数单调性即可求出
在[1,3]是单调递减函数,利用函数单调性即可求出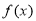 在[1,3]上的最小值及对应的
在[1,3]上的最小值及对应的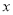 值;当
值;当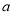 小于3时,由(1)知
小于3时,由(1)知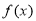 在[1,
在[1, 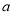 ]是减函数,在[
]是减函数,在[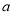 ,3]是增函数,故当
,3]是增函数,故当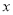 =
=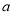 时,
时,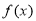 取最小值,即可求得最小值
取最小值,即可求得最小值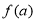 .
.
试题解析:(1)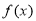 的定义域为
的定义域为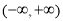 ,
,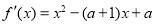 1分
1分
令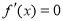 ,得
,得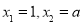
令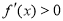 ,得
,得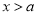 或
或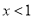 2分
2分
令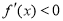 ,得
,得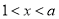 3分
3分
故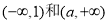 为
为 单调递增区间,
单调递增区间, 为
为 单调递减区间. 5分
单调递减区间. 5分
(2)因为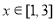 ,所以
,所以
(ⅰ)当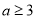 时,由(1)知,
时,由(1)知,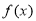 在[1,3]上单调递减, 7分
在[1,3]上单调递减, 7分
所以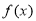 在
在 时取得最小值, 8分
时取得最小值, 8分
最小值为: 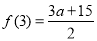 9分
9分
(ⅱ)当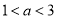 时,
时,
由(Ⅰ)知,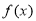 在[0,
在[0,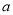 ]上单调递减,在[
]上单调递减,在[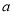 ,3]上单调递增, 11分
,3]上单调递增, 11分
所以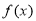 在
在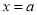 处取得最小值,最小值为: 12分
处取得最小值,最小值为: 12分
又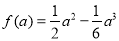 , 13分
, 13分
所以当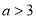 时,
时,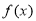 在
在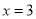 处取得最小值
处取得最小值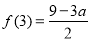 ;
;
当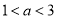 时,
时,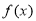 在
在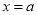 处取得最小值
处取得最小值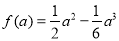 . 14分
. 14分
考点:常见函数的导数;函数单调性与导数的关系;函数的最值;分类整合思想


科目:高中数学 来源:2015届广西桂林中学高二下学期期中考试文科数学试卷(解析版) 题型:选择题
对任意的x∈R,函数f(x)=x3+ax2+7ax不存在
极值点的充要条件是( )
A.a=0或a=7 B.a<0或a>21 C.0≤a≤21 D.a=0或a=21
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com