Question

7．正三棱锥O-ABC的每一条棱长均为1，若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$（0≤x，y，z≤1），且满足1≤x+y+z≤2，则动点P的轨迹所围成的区域的体积是$\frac{\sqrt{2}}{3}$．

Answer 1

分析 由已知可得动点P的轨迹所围成的区域，然后由柱体体积减去两个三棱锥的体积得答案．

解答 解：如图，由$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$（0≤x，y，z≤1），且满足1≤x+y+z≤2，
可得动点P的轨迹所围成的区域是介于平面ABC与平面EFG之间的部分，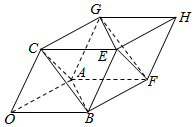

∴$V=OA•OB•sin60°•{h}_{C}-2•\frac{1}{3}{S}_{△OAB}•{h}_{C}$
=$1×1×\frac{\sqrt{3}}{2}×\frac{\sqrt{6}}{3}-2×\frac{1}{3}×\frac{1}{2}×\frac{\sqrt{3}}{2}×\frac{\sqrt{6}}{3}$=$\frac{\sqrt{2}}{3}$．
故答案为：$\frac{\sqrt{2}}{3}$．

点评 本题考查空间向量的坐标加法运算，考查柱、锥、台体积的求法，由已知向量等式得到点P的轨迹所围成的区域是关键，是中档题．