
分析 先可将原函数变成y=$(cosx+\frac{1}{2})^{2}-\frac{5}{4}$,而由x的范围,根据余弦函数的图象可求出$cosx∈[-\frac{1}{2},1]$,通过上面函数解析式即可求出原函数的最大值,最小值,从而求出其值域.
解答 解:y=cos2x+cosx-1=$(cosx+\frac{1}{2})^{2}-\frac{5}{4}$;
$x∈[-\frac{π}{3},\frac{2π}{3}]$,
∴$cosx∈[-\frac{1}{2},1]$;
∴$cosx=-\frac{1}{2}$时,原函数取最小值$-\frac{5}{4}$;
cosx=1时,原函数取最大值1;
∴原函数的值域为$[-\frac{5}{4},1]$.
故答案为:[$-\frac{5}{4}$,1].
点评 考查sin2x+cos2x=1,配方法求函数的最值,从而求出函数的值域,以及对余弦函数图象的掌握,根据余弦函数的图象求余弦函数的范围.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{3}{2},2}]$ | B. | $[{-2,\frac{3}{2}}]$ | C. | $[{-2,-\frac{3}{2}}]$ | D. | $[{\frac{3}{2},2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2014年12月28日开始,北京市公共电汽车和地铁按照里程分段计价.具体如下表.(不考虑公交卡折扣情况)
2014年12月28日开始,北京市公共电汽车和地铁按照里程分段计价.具体如下表.(不考虑公交卡折扣情况)| 乘公共电汽车方案 | 10公里(含)内2元; 10公里以上部分,每增加1元可乘坐5公里(含). |
乘坐地铁方案(不含机场线) | 6公里(含)内3元; 6公里至12公里(含)4元; 12公里至22公里(含)5元; 22公里至32公里(含)6元; 32公里以上部分,每增加1元可乘坐20公里(含). |
查看答案和解析>>
科目:高中数学 来源:2017届云南曲靖市高三上半月考一数学试卷(解析版) 题型:解答题
已知命题 :指数函数
:指数函数 在
在 上单调递减,命题
上单调递减,命题 :关于
:关于 的方程
的方程 的两个实根均大于
的两个实根均大于 .若
.若 或
或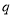 为真,
为真, 且
且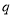 为假,求实数
为假,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com