练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知sinα+cosα=$\frac{1}{2}$，求下列各式的值：
    （1）sinαcosα；
    （2）sin3α+cos3α

    分析 （1）已知等式两边平方，利用完全平方公式及同角三角函数间基本关系化简，整理即可求出原式的值；
    （2）原式利用立方和公式变形，将各自的值代入计算即可求出值．

    解答 解：（1）把sinα+cosα=$\frac{1}{2}$两边平方得：
    （sinα+cosα）2=sin2α+2sinαcosα+cos2α=1+2sinαcosα=$\frac{1}{4}$，
    则sinαcosα=-$\frac{3}{8}$；
    （2）原式=（sinα+cosα）（sin2α-sinαcosα+cos2α）=（sinα+cosα）（1-sinαcosα）=$\frac{11}{16}$．

    点评 此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    20．已知数列{an}中对于任意正整数n都有an+1=${a}_{n}^{2}$+can，其中c为实常数．
    （Ⅰ）若c=2，a1=1，求数列{an}的通项公式；
    （Ⅱ）若c=0，记Tn=（a1-a2）a3+（a2-a3）a4+…+（an-an+1）an+2，证明：
    1）当0＜a1≤$\frac{1}{2}$时，Tn＜$\frac{1}{32}$；
    2）当$\frac{1}{2}$＜a1＜1时，Tn＜$\frac{1}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=$\frac{1}{2}$ax2+4x-lnx．
    （1）当a=-3时，求f（x）的单调区间；
    （2）当a≠0时，若f（x）是减函数，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知f（x）=$\left\{\begin{array}{l}{|lnx|，x＞0}\\{x+2，x≤0}\end{array}\right.$，若关于x的方程f2（x）-af（x）+b=0有6个不同的解，则a的取值范围为（　　）
    A．（0，3）B．（0，4）C．（0，4]D．[1，4]

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．若x2+4y2=5，则x+y的最小值为$-\frac{5}{2}$，最小值点为（-2，$-\frac{1}{2}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

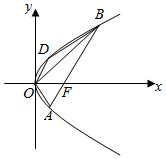    15．如图所示，已知抛物线C：y2=4x的焦点是F，直线l经过点F交抛物线C于A，B两点，A点在x轴下方，点D和点A关于x轴对称．
    （1）若$\overrightarrow{BF}$=4$\overrightarrow{FA}$，求直线l的方程；
    （2）求S2△OAF+S2△OBD的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知向量$\overrightarrow{a}$=（cosx，sinx），$\overrightarrow{b}$=（cosx，-sinx）．
    （1）若函数f（x）=2$\overrightarrow{a}$•$\overrightarrow{b}$+1，求函数f（x）的周期和最值；
    （2）若$\overrightarrow{a}$∥$\overrightarrow{b}$，且x∈[$\frac{π}{6}$，$\frac{2π}{3}$]，求x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=$\frac{1}{x}$-alnx（a∈R）．
    （Ⅰ）若h（x）=f（x）-2x，当a=-3时，求h（x）的单调递减区间；
    （Ⅱ）若函数f（x）有唯一的零点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．若关于x的方程sinx+$\sqrt{3}$cosx+a=0在（0，2π）内有两个不同的实数根α，β，求实数a的取值范围及相应的α+β的值．

    查看答案和解析>>

    同步练习册答案