
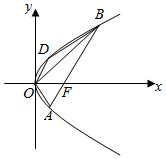
 如图所示,已知抛物线C:y2=4x的焦点是F,直线l经过点F交抛物线C于A,B两点,A点在x轴下方,点D和点A关于x轴对称.
如图所示,已知抛物线C:y2=4x的焦点是F,直线l经过点F交抛物线C于A,B两点,A点在x轴下方,点D和点A关于x轴对称.分析 (1)设出A、B坐标,利用$\overrightarrow{BF}$=4$\overrightarrow{FA}$,求出A、B坐标之间的关系,然后求直线l的方程;
(2)求出S2OAF+S2△OBD的表达式,利用基本不等式求S2OAF+S2△OBD的最小值.
解答 解:(1)设A,B两点坐标为A(x1,y1),B(x2,y2),
∵$\overrightarrow{BF}$=4$\overrightarrow{FA}$,
∴(1-x2,-y2)=4(x1-1,y1),
∴1-x2=4(x1-1),-y2=4y1…①
由题意,设直线AB的方程为y=k(x-1),代入抛物线方程,得ky2-4y-4k=0,
因为直线l与C相交于A,B两点,所以k≠0,
则△=16+16k2>0,y1+y2=$\frac{4}{k}$,y1y2=-4,…②
由①②,得方程组k=±$\frac{4}{3}$,
∵A点在x轴下方,
∴直线l的方程为y=$\frac{4}{3}$(x-1);
(2)直线OB的方程为y=$\frac{{y}_{2}}{{x}_{2}}$x,即2px-y2y=0,
∵点D和点A关于x轴对称,
∴D(x1,-y1),
∴D到直线OB的距离d=$\frac{|2p{x}_{1}+{y}_{1}{y}_{2}|}{\sqrt{4{p}^{2}+{{y}_{2}}^{2}}}$=$\frac{|2p{x}_{1}-4|}{\sqrt{2p(2p+{x}_{2})}}$,
∴S2△OBD=x2(x1-1)2,
∵直线AB的方程为y=k(x-1),代入抛物线方程,得k2x2-(2k2+4)x+k2=0,
∴x1x2=1
∵S2OAF=$\frac{1}{4}$×1×y12=x1,
∴S2OAF+S2△OBD=x1+=2x1+$\frac{1}{{x}_{1}}$-2≥2$\sqrt{2}$-2,
当且仅当2x1=$\frac{1}{{x}_{1}}$,即x1=$\frac{\sqrt{2}}{2}$时,S2OAF+S2△OBD的最小值为2$\sqrt{2}$-2
点评 本题考查直线与抛物线的方程,考查向量知识的运用,考查三角形面积的计算,考查基本不等式的运用,考查转化思想,函数与方程的思想.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小正周期为π的偶函数 | B. | 最小正周期为π的奇函数 | ||
| C. | 最小正周期为2π的偶函数 | D. | 最小正周期为2π的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com