
分析 把已知等式变形,然后利用三角换元,借助于辅助角公式化简求得答案.
解答 解:由x2+4y2=5,得$(\frac{x}{\sqrt{5}})^{2}+(\frac{2y}{\sqrt{5}})^{2}=1$,
令$\frac{x}{\sqrt{5}}=cosθ,\frac{2y}{\sqrt{5}}=sinθ$,得$x=\sqrt{5}cosθ,y=\frac{\sqrt{5}}{2}sinθ$,
∴$x+y=\frac{\sqrt{5}}{2}sinθ+\sqrt{5}cosθ$=$\frac{5}{2}sin(θ+α)$(tanα=2,α为锐角).
∴x+y的最小值为-$\frac{5}{2}$,此时sin(θ+α)=-1,即θ+α=$-\frac{π}{2}+2kπ$,k∈Z.
$θ=-\frac{π}{2}-α+2kπ$,k∈Z.
则x=$\sqrt{5}cosθ=\sqrt{5}cos(-\frac{π}{2}-α+2kπ)$=$\sqrt{5}cos(\frac{π}{2}+α)=-\sqrt{5}sinα$=$-\sqrt{5}×\frac{2}{\sqrt{5}}=-2$.
∴y=-$\frac{1}{2}$,最小值点为($-2,-\frac{1}{2}$).
故答案为:$-\frac{5}{2}$;($-2,-\frac{1}{2}$).
点评 本题考查函数最值的求法,训练了换元法,属中档题.


科目:高中数学 来源: 题型:选择题
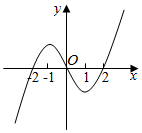 已知R上的可导函数f(x)的图象如图所示,两个极值点分别为-1和1,若f′(x)为函数f(x)的导函数,则不等式(x2-2x-3)f′(x)>0的解集为( )
已知R上的可导函数f(x)的图象如图所示,两个极值点分别为-1和1,若f′(x)为函数f(x)的导函数,则不等式(x2-2x-3)f′(x)>0的解集为( )| A. | (-∞,-2)∪(1,+∞) | B. | (-∞,-1)∪(-1,1)∪(3,+∞) | C. | (-∞,-1)∪(-1,0)∪(2,+∞) | D. | (-∞,-2)∪(1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (0,1) | C. | (-2,2) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com