
分析 由sinx+$\sqrt{3}$cosx+a=0,得sinx+$\sqrt{3}$cosx=-a,画出函数y=sinx+$\sqrt{3}$cosx=$2sin(x+\frac{π}{3})$的图象,数形结合得答案.
解答 解:由sinx+$\sqrt{3}$cosx+a=0,得sinx+$\sqrt{3}$cosx=-a,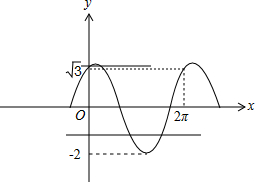
令y=sinx+$\sqrt{3}$cosx=$2sin(x+\frac{π}{3})$,
∵x∈(0,2π),∴x+$\frac{π}{3}$∈($\frac{π}{3}$,$\frac{7π}{3}$),
作出函数$y=2sin(x+\frac{π}{3})$的图象如图:
若关于x的方程sinx+$\sqrt{3}$cosx+a=0在(0,2π)内有两个不同的实数根α,β,
则-2$<-a<\sqrt{3}$,或$\sqrt{3}<-a<2$,
即$-2<a<-\sqrt{3}$或$-\sqrt{3}<a<2$.
当a∈(-2,-$\sqrt{3}$)时,$α+β=\frac{π}{3}$;
当a∈(-$\sqrt{3}$,2)时,$α+β=\frac{7π}{3}$.
点评 本题考查三角函数中的恒等变换应用,考查y=Asin(ωx+φ)型函数的图象和性质,训练了数形结合的解题思想方法,是中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com