
| A. | {-2,2} | B. | {0,2} | C. | {2} | D. | {0,-2,2} |
分析 判断角所在的象限,然后去掉绝对值求解即可.
解答 解:角α的终边在第一象限,则$\frac{α}{2}$∈(k$π,kπ+\frac{π}{4}$),k∈Z,
$\frac{α}{2}$在第一象限时,$\frac{sin\frac{α}{2}}{|sin\frac{α}{2}|}$+$\frac{cos\frac{α}{2}}{|cos\frac{α}{2}|}$=2,
当$\frac{α}{2}$在第三象限时,则$\frac{sin\frac{α}{2}}{|sin\frac{α}{2}|}$+$\frac{cos\frac{α}{2}}{|cos\frac{α}{2}|}$=-2.
则$\frac{sin\frac{α}{2}}{|sin\frac{α}{2}|}$+$\frac{cos\frac{α}{2}}{|cos\frac{α}{2}|}$的取值集合为:{2,-2}.
故选:A.
点评 本题考查三角函数化简求值,注意交所在象限,考查计算能力.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:高中数学 来源: 题型:选择题
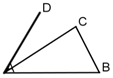
| A. | α≤β<π | B. | α≤β≤π-α | C. | $\frac{π}{2}-α≤β<π$ | D. | $\frac{π}{2}-α≤β≤π-α$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{1}{4}]$ | B. | $(-∞,\frac{1}{4})$ | C. | (-2,0) | D. | [-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
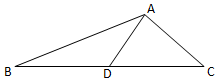 △ABC中,角A,B,C的对边分别为a,b,c,A=$\frac{3π}{4}$,sinB=$\frac{\sqrt{10}}{10}$,D为BC边中点,AD=1.
△ABC中,角A,B,C的对边分别为a,b,c,A=$\frac{3π}{4}$,sinB=$\frac{\sqrt{10}}{10}$,D为BC边中点,AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com