练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知a≥0且{y|y=2|x|，-2≤x≤a}=[m，n]，记g（a）=n-m，则g（a）=$g（a）=\left\{\begin{array}{l}3，0≤a≤2\\{2^a}-1，a＞2\end{array}\right.$．

    分析 根据指数函数的性质求得m、n的值；然后代入求值．

    解答 解：①当0≤a≤2时，m=4，n=1，则g（a）=n-m=3；
    ②当a＞2时，m=2a，n=1，则g（a）=n-m=2a-1，
    综上所述，$g（a）=\left\{\begin{array}{l}3，0≤a≤2\\{2^a}-1，a＞2\end{array}\right.$．
    故答案是：$g（a）=\left\{\begin{array}{l}3，0≤a≤2\\{2^a}-1，a＞2\end{array}\right.$．

    点评 本题考查了集合相等．根据指数的性质求得m、n的值是解题的关键，解题时，注意对a的取值范围要进行分类讨论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．某工厂2015年生产某产品2万件，计划从2016年开始每年比上一年增产20%，从哪一年开始这家工厂生产这种产品的年产量超过6万件（已知lg2=0.3010，lg3=0.4771）（　　）
    A．2019年B．2020年C．2021年D．2022年

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．不等式1≤|2x-1|＜2的解集为（　　）
    A．$（{-\frac{1}{2}，0}）∪[{1，\frac{3}{2}}）$B．$（{-\frac{1}{2}，\frac{3}{2}}）$C．$（{-\frac{1}{2}，0}]∪[{1，\frac{3}{2}}）$D．（-∞，0]∪[1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

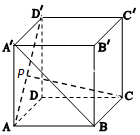    18．如图，在正方体ABCD-A'B'C'D'中，点P在线段AD'上，且AP≤$\frac{1}{2}$AD'则异面直线CP与BA'所成角θ的取值范围是[$\frac{π}{6}$，$\frac{π}{3}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．函数f（x）=e-|x-1|的图象是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若函数f（x）=x2+2（a-1）x+2在区间[-1，2]上单调，则实数a的取值范围为（　　）
    A．[2，+∞）B．（-∞，-1]C．（-∞，-1]∪[2，+∞）D．（-∞，-1）∪（2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．角α的终边在第一象限，则$\frac{sin\frac{α}{2}}{|sin\frac{α}{2}|}$+$\frac{cos\frac{α}{2}}{|cos\frac{α}{2}|}$的取值集合为（　　）
    A．{-2，2}B．{0，2}C．{2}D．{0，-2，2}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．若函数f（x）=ex（sinx+a）在区间（0，π）上单调递减，则实数a的取值范围是（　　）
    A．[-$\sqrt{2}$，+∞）B．[1，+∞）C．（-∞，-$\sqrt{2}$]D．（-∞，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．若函数f（x）=$\left\{\begin{array}{l}{-x+3，-1≤x≤1}\\{1+lo{g}_{（{a}^{2}-1）}（2x），2≤x≤8}\end{array}\right.$的值域是[2，5]，则实数a的取值是$±\sqrt{3}$．

    查看答案和解析>>

    同步练习册答案