
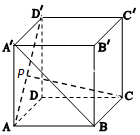
 如图,在正方体ABCD-A'B'C'D'中,点P在线段AD'上,且AP≤$\frac{1}{2}$AD'则异面直线CP与BA'所成角θ的取值范围是[$\frac{π}{6}$,$\frac{π}{3}$].
如图,在正方体ABCD-A'B'C'D'中,点P在线段AD'上,且AP≤$\frac{1}{2}$AD'则异面直线CP与BA'所成角θ的取值范围是[$\frac{π}{6}$,$\frac{π}{3}$]. 分析 如图,连结CD',则异面直线CP与BA'所成的角θ等于∠D'CP,由图可知,当P点与A点重合时,可得θ=$\frac{π}{3}$.当P点无限接近D'点时,θ趋近于0,由于AP≤$\frac{1}{2}$AD',故得P在AD'中点时,θ最小,即可得到范围.
解答 解:如图,ABCD-A'B'C'D'是正方体,连结CD',则异面直线CP与BA'所成的角θ等于∠D'CP,
由图可知,当P点与A点重合时,可得θ=$\frac{π}{3}$.
当P点无限接近D'点时,θ趋近于0,
∵AP≤$\frac{1}{2}$AD',故得P在AD'中点时,θ最小,
设正方体的边长为1,则AD'=$\sqrt{2}$,CD'=$\sqrt{2}$,PC=$\frac{\sqrt{6}}{2}$
AP=$\frac{1}{2}$AD'=$\frac{\sqrt{2}}{2}$,
即:$cosθ=\frac{D′{C}^{2}+C{P}^{2}-D′{P}^{2}}{2D′C•CP}$=$\frac{\sqrt{3}}{2}$
∴$θ=\frac{π}{6}$.
所以异面直线CP与BA'所成角θ的取值范围是[$\frac{π}{6}$,$\frac{π}{3}$].
故答案为:[$\frac{π}{6}$,$\frac{π}{3}$].
点评 本题考查了空间动点的变化,异面直线所成角的问题.找到所成的角,当P点移动是,观察角的变化情况.属于中档题.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
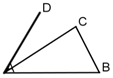
| A. | α≤β<π | B. | α≤β≤π-α | C. | $\frac{π}{2}-α≤β<π$ | D. | $\frac{π}{2}-α≤β≤π-α$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥1} | B. | {x|x≥-1} | C. | {x|-1≤x≤2} | D. | {x|1≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com