
分析 (1)通过设出甲投资以及乙投资的数目,设立函数表达式,根据函数式直接写出定义域;
(2)对于(1)中的函数解析式,利用换元法转化成一个二次函数的形式,最后结合二次函数的最值求法得出函数的最大值,从而解决问题.
解答 解:(1)$y=\frac{1}{5}x+\frac{3}{5}\sqrt{3-x}$(0≤x≤3)…6分
(2)设$\sqrt{3-x}=t$,x=3-t2,因为0≤x≤3,所以$0≤t≤\sqrt{3}$,…8分$y=\frac{1}{5}(3-{t^2})+\frac{3}{5}t=-\frac{1}{5}{t^2}+\frac{3}{5}t+\frac{3}{5}=-\frac{1}{5}{(t-\frac{3}{2})^2}+\frac{21}{20}$.$(0≤t≤\sqrt{3})$…12分
当$t=\frac{3}{2}$时,即 $x=\frac{3}{4}$时,${y_{max}}=\frac{21}{20}$.…13分
答:应甲种商品投资$\frac{3}{4}$万元,对乙种商品投资$\frac{9}{4}$万元时,总利润最大,最大值为$\frac{21}{20}$万元.…14分.
点评 本题考查函数模型的选择与应用,通过对实际问题的分析,构造数学模型从而解决问题.需要对知识熟练的掌握并应用,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
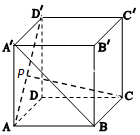 如图,在正方体ABCD-A'B'C'D'中,点P在线段AD'上,且AP≤$\frac{1}{2}$AD'则异面直线CP与BA'所成角θ的取值范围是[$\frac{π}{6}$,$\frac{π}{3}$].
如图,在正方体ABCD-A'B'C'D'中,点P在线段AD'上,且AP≤$\frac{1}{2}$AD'则异面直线CP与BA'所成角θ的取值范围是[$\frac{π}{6}$,$\frac{π}{3}$].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\sqrt{2}$,+∞) | B. | [1,+∞) | C. | (-∞,-$\sqrt{2}$] | D. | (-∞,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
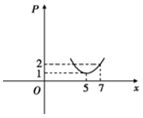 某产品关税与市场供应量P的关系近似地满足:P(x)=2${\;}^{(1-kt){{(x-b)}{\;}^2}}}$(其中t为关税的税率,且t∈[0,$\frac{1}{2}}$],x为市场价格,b,k为正常数),当t=$\frac{1}{8}$时,市场供应量曲线如图所示:
某产品关税与市场供应量P的关系近似地满足:P(x)=2${\;}^{(1-kt){{(x-b)}{\;}^2}}}$(其中t为关税的税率,且t∈[0,$\frac{1}{2}}$],x为市场价格,b,k为正常数),当t=$\frac{1}{8}$时,市场供应量曲线如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com