
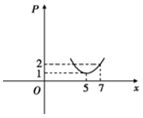
 ij��Ʒ��˰���г���Ӧ��P�Ĺ�ϵ���Ƶ����㣺P��x��=2${\;}^{��1-kt��{{��x-b��}{\;}^2}}}$������tΪ��˰��˰�ʣ���t��[0��$\frac{1}{2}}$]��xΪ�г��۸�b��kΪ������������t=$\frac{1}{8}$ʱ���г���Ӧ��������ͼ��ʾ��
ij��Ʒ��˰���г���Ӧ��P�Ĺ�ϵ���Ƶ����㣺P��x��=2${\;}^{��1-kt��{{��x-b��}{\;}^2}}}$������tΪ��˰��˰�ʣ���t��[0��$\frac{1}{2}}$]��xΪ�г��۸�b��kΪ������������t=$\frac{1}{8}$ʱ���г���Ӧ��������ͼ��ʾ������ ��1���ܸ���ͼ��֪$t=\frac{1}{8}$ʱ����$\left\{\begin{array}{l}{2^{��1-\frac{k}{8}��{{��5-b��}^2}}}=1\\{2^{��1-\frac{k}{8}��{{��7-b��}^2}}}=2\end{array}\right.$���������k��b��ֵ��
��2���ܸ�������캯���������ڶ���������������Сֵ��
��� �⣺��1����ͼ��֪$t=\frac{1}{8}$ʱ����$\left\{\begin{array}{l}{2^{��1-\frac{k}{8}��{{��5-b��}^2}}}=1\\{2^{��1-\frac{k}{8}��{{��7-b��}^2}}}=2\end{array}\right.$���$\left\{\begin{array}{l}k=6\\ b=5.\end{array}\right.$
��2����P=Qʱ����${2^{��1-6t��{{��x-5��}^2}}}={2^{11-\frac{1}{2}x}}$��
���$t=\frac{1}{6}[{1-\frac{22-x}{{2{{��x-5��}^2}}}}]=-\frac{1}{12}[{\frac{17}{{{{��x-5��}^2}}}-\frac{1}{x-5}-2}]$��
��$m=\frac{1}{x-5}$����x��9����$m�ʣ�0��\frac{1}{4}]$��
��$t=-\frac{1}{12}��17{m^2}-m-2��$�У��Գ���Ϊֱ��$m=\frac{1}{34}$��$\frac{1}{34}�ʣ�0��\frac{1}{4}]$����ͼ�����£�
��$m=\frac{1}{4}$ʱ��tȡ����Сֵ$\frac{19}{192}$����ʱx=9��
���� �����Ǹ�ָ���������ۺ��⣬�������Ĺ�����Ҳ�õ��˹��캯����˼�뼰���κ����ڶ�����������ֵ��֪ʶ�������֪ʶȫ�����λ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3$\sqrt{3}$ | C�� | 2$\sqrt{3}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $[{\frac{��}{12}��\frac{��}{6}}]$ | B�� | $[{\frac{��}{6}��\frac{��}{2}}]$ | C�� | $[{\frac{��}{12}��\frac{��}{3}}]$ | D�� | $[{\frac{��}{6}��\frac{��}{3}}]$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com