
分析 (1)利用导数的正负,即可证明;
(2)求出g(x)=x+$\frac{4}{x}$,又g(x)的定义域为(-∞,0)∪(0,+∞)关于原点对称,利用奇函数的定义进行判断;
(3)由(2)知f(x)=m可化为x+$\frac{4}{x}$=m-4(m≥8),再分类讨论,即可得出结论.
解答 证明:(1)由题意:f(x)=x+$\frac{4}{x}$+a,
∴f′(x)=$\frac{{x}^{2}-4}{{x}^{2}}$,
∴0<x<2时,f′(x)<0,x>2时,f′(x)>0,
∴函数f(x)在(0,2]上是减函数,(2,+∞)上是增函数 …(4分)
解:(2)由题意知方程x2+ax+4=0有且只有一个实数根
∴△=a2-16=0,
又a>0,∴a=4.…(5分)
此时f(x)=x+$\frac{4}{x}$+4,g(x)=x+$\frac{4}{x}$,
又g(x)的定义域为(-∞,0)∪(0,+∞)关于原点对称,…(6分)
且g(-x)=-x-$\frac{4}{x}$=-g(x),…(7分)
∴g(x)是奇函数 …(8分)
(3)由(2)知f(x)=m可化为x+$\frac{4}{x}$=m-4(m≥8)…(9分)
又由(1)(2)知:
当m-4=4 即m=8时f(x)=m只有一解 …(10分)
当m-4>4即m>8时f(x)=m有两解 …(11分)
综上,当m=8时f(x)=m只有一解;当m>8时f(x)=m有两解; …(12分)
点评 本题考查函数的单调性与奇偶性,考查方程解的个数的判断,属于中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | (-∞,-1] | C. | (-∞,-1]∪[2,+∞) | D. | (-∞,-1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
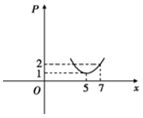 某产品关税与市场供应量P的关系近似地满足:P(x)=2${\;}^{(1-kt){{(x-b)}{\;}^2}}}$(其中t为关税的税率,且t∈[0,$\frac{1}{2}}$],x为市场价格,b,k为正常数),当t=$\frac{1}{8}$时,市场供应量曲线如图所示:
某产品关税与市场供应量P的关系近似地满足:P(x)=2${\;}^{(1-kt){{(x-b)}{\;}^2}}}$(其中t为关税的税率,且t∈[0,$\frac{1}{2}}$],x为市场价格,b,k为正常数),当t=$\frac{1}{8}$时,市场供应量曲线如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{1}{x}$ | B. | y=1g|x| | C. | y=cosx | D. | y=x2+2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com