【题目】在平面直角坐标系
中，曲线
(
为参数，实数
)，曲线
(为参数，实数
)．在以
为极点，
轴的正半轴为极轴的极坐标系中，射线
与
交于，
两点，与
交于，
两点．当
时，
；当
时，
.
(Ⅰ)求
，
的值及曲线 和极坐标方程；
(Ⅱ)求
的最大值
【答案】(Ⅰ) 见解析 (Ⅱ) 
【解析】
（I）根据平方法消去参数可得到曲线C1，
的普通方程，再利用极坐标与直角坐标互化公式即可得出极坐标方程，进而得a和b的值．
（II）利用C1，C2的极坐标方程可得
，利用二倍角公式和辅助角公式进行化简，然后利用正弦函数图像的性质即可得到最大值．
(Ⅰ)由曲线
(
为参数，实数
)，
化为普通方程为
，展开为：
，
其极坐标方程为
，即
，
由题意可得当
时，
，∴
.
曲线
极坐标方程为
曲线
(为参数，实数
)，
化为普通方程为
，展开可得极坐标方程为
，
由题意可得当
时，
，∴
.
曲线极坐标方程为
(Ⅱ)由(Ⅰ)可得
，的极坐标方程分别为，.
∴
，
∵
，
∴
的最大值为，
当
，
时取到最大值.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】据统计，仅在北京地区每天就有500万单快递等待派送，近5万多名快递员奔跑在一线，快递网点人员流动性也较强，各快递公司需要经常招聘快递员，保证业务的正常开展．下面是50天内甲、乙两家快递公司的快递员每天送货单数统计表：
送货单数 | 30 | 40 | 50 | 60 | |
天数 | 甲 | 10 | 10 | 20 | 10 |
乙 | 6 | 14 | 24 | 6 | |
已知这两家快递公司的快递员日工资方案分别为：甲公司规定底薪
元，每单抽成
元；乙公司规定底薪
元，每日前
单无抽成，超过单的部分每单抽成
元．
（1）分别求甲、乙快递公司的快递员的日工资
（单位：元）与送货单数
的函数关系式；
（2）小赵拟到甲、乙两家快递公司中的一家应聘快递员的工作，如果仅从日收入的角度考虑，以这50天的送货单数为样本，将频率视为概率，请你利用所学的统计学知识为他作出选择，并说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率为
，以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2
。
（1）求椭圆的方程；
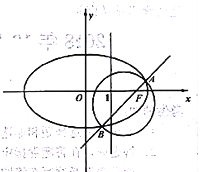
（2）如图，斜率为k的直线l过椭圆的右焦点F，且与椭圆交与A，B两点，以线段AB为直径的圆截直线x＝1所得的弦的长度为
，求直线l的方程。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分12分）一个盒子里装有三张卡片，分别标记有数字
，
，
，这三张卡片除标记的数字外完全相同。随机有放回地抽取次，每次抽取张，将抽取的卡片上的数字依次记为
，
，
.
（Ⅰ）求“抽取的卡片上的数字满足
”的概率；
（Ⅱ）求“抽取的卡片上的数字，，不完全相同”的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中, 曲线
的参数方程为
为参数) ；在以原点
为极点, 
轴的正半轴为极轴的极坐标系中, 曲线
的极坐标参数方程为
.
（1）求曲线
的极坐标方程和曲线
的直角坐标方程；
（2）若射线
与曲线
,
的交点分别为
(
异于原点). 当斜率
时, 求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在某次数学考试中，小江的成绩在90分以上的概率是0.25，在
的概率是0.48，在
的概率是0.11，在
的概率是0.09，在60分以下的概率是0.07.计算：
（1）小江在此次数学考试中取得80分及以上的概率；
（2）小江考试及格（成绩不低于60分）的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数f（x）＝Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜
）的图象如图所示，为了得到g（x）＝Acosωx的图象，只需把y＝f（x）的图象上所有的点（ ）
A. 向右平移
个单位长度 B. 向左平移个单位长度
C. 向右平移
个单位长度 D. 向左平移个单位长度
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
过点
，且其中一个焦点的坐标为
.
（1）求椭圆
的方程；
（2）过椭圆右焦点
的直线
与椭圆交于两点
，在
轴上是否存在点
，使得
为定值？若存在，求出点的坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
