
【题目】在平面直角坐标系![]() 中, 曲线
中, 曲线![]() 的参数方程为
的参数方程为![]() 为参数) ;在以原点
为参数) ;在以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中, 曲线
轴的正半轴为极轴的极坐标系中, 曲线![]() 的极坐标参数方程为
的极坐标参数方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 与曲线
与曲线![]() ,
,![]() 的交点分别为
的交点分别为![]() (
(![]() 异于原点). 当斜率
异于原点). 当斜率![]() 时, 求
时, 求![]() 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某种商品原来每件售价为25元,年销售量8万件.
(Ⅰ)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收人不低于原收入,该商品每件定价最多为多少元?
(Ⅱ)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到x元.公司拟投入 ![]() (x2﹣600)万元作为技改费用,投入50万元作为固定宣传费用,投入
(x2﹣600)万元作为技改费用,投入50万元作为固定宣传费用,投入 ![]() x万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
x万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}中,a2=2,a5=128.
(1)求通项an;
(2)若bn=log2an , 数列{bn}的前n项和为Sn , 且Sn=360,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足:bn=an+1-an(n∈N*).
(1)若a1=1,bn=n,求数列{an}的通项公式;
(2)若bn+1bn-1=bn(n≥2),且b1=1,b2=2.
(ⅰ)记cn=a6n-1(n≥1),求证:数列{cn}为等差数列;
(ⅱ)若数列![]() 中任意一项的值均未在该数列中重复出现无数次,求首项a1应满足的条件.
中任意一项的值均未在该数列中重复出现无数次,求首项a1应满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( ) 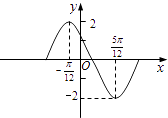
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
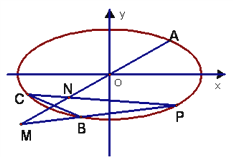
【题目】如图,在平面直角坐标系中,已知A、B、C是椭圆![]() 上不同的三点,
上不同的三点,  ,C在第三象限,线段BC的中点在直线OA上。
,C在第三象限,线段BC的中点在直线OA上。
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点P在椭圆上(异于点A、B、C)且直线PB, PC分别交直线OA于M、N两点,证明![]() 为定值并求出该定值.
为定值并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标.
的坐标.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ
的夹角θ
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com