
【题目】已知数列{an},{bn}满足:bn=an+1-an(n∈N*).
(1)若a1=1,bn=n,求数列{an}的通项公式;
(2)若bn+1bn-1=bn(n≥2),且b1=1,b2=2.
(ⅰ)记cn=a6n-1(n≥1),求证:数列{cn}为等差数列;
(ⅱ)若数列![]() 中任意一项的值均未在该数列中重复出现无数次,求首项a1应满足的条件.
中任意一项的值均未在该数列中重复出现无数次,求首项a1应满足的条件.
【答案】(1)an=![]() (2)(ⅰ)详见解析(ⅱ)详见解析
(2)(ⅰ)详见解析(ⅱ)详见解析
【解析】
试题分析:(1)利用叠加法求数列{an}的通项公式:an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=a1+b1+b2+…+bn-1=![]() (2)(ⅰ)利用定义证等差数列:cn+1-cn=
(2)(ⅰ)利用定义证等差数列:cn+1-cn=
a6n+5-a6n-1为常数,由bn+1bn-1=bn得{bn}为周期数列,再由bn=an+1-an得a6n+5-a6n-1=b6n-1+b6n+b6n+1+b6n+2+b6n+3+b6n+4=7(ⅱ)由(ⅰ)知数列{a6(n-1)+i}均为以7为公差的等差数列,而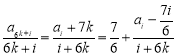 ,因此ai=
,因此ai=![]() 时,重复出现无数次,因此
时,重复出现无数次,因此![]() 依次类推得a1∈{
依次类推得a1∈{![]() ,
,![]() ,
,![]() ,-
,-![]() ,-
,-![]() }数列
}数列![]() 中必有某数重复出现无数次;当a1B时,最多出现一次
中必有某数重复出现无数次;当a1B时,最多出现一次
试题解析:解:(1)当n≥2时,有an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=a1+b1+b2+…+bn-1=![]()
又a1=1也满足上式,所以数列{an}的通项公式是an=![]()
(2)(ⅰ)因为对任意的n∈N*,有bn+6=![]() =bn,
=bn,
所以cn+1-cn=a6n+5-a6n-1
=b6n-1+b6n+b6n+1+b6n+2+b6n+3+b6n+4
=1+2+2+1+![]() +
+![]() =7
=7
所以,数列{cn}为等差数列.
(ⅱ)设cn=a6(n-1)+i(n∈N*)(其中i为常数且i∈{1,2,3,4,5,6},
所以cn+1-cn=a6(n-1)+6+i-a6(n-1)+i
=b6(n-1)+i+b6(n-1)+i+1+b6(n-1)+i+2+b6(n-1)+i+3+b6(n-1)+i+4+b6(n-1)+i+5=7,
即数列{a6(n-1)+i}均为以7为公差的等差数列.
设fk=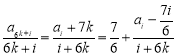 (其中n=6k+i, k≥0,
(其中n=6k+i, k≥0,
i为{1,2,3,4,5,6}中一个常数)
当ai=![]() 时,对任意的n=6k+i,有
时,对任意的n=6k+i,有![]() ;
;
当ai≠![]() 时,fk+1-fk=
时,fk+1-fk=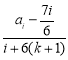 -
-![]() =
=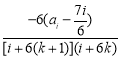
①若ai>![]() ,则对任意的k∈N有fk+1<fk,所以数列{
,则对任意的k∈N有fk+1<fk,所以数列{![]() }为递减数列;
}为递减数列;
②若ai<![]() ,则对任意的k∈N有fk+1>fk,所以数列{
,则对任意的k∈N有fk+1>fk,所以数列{![]() }为递增数列.
}为递增数列.
综上所述,集合B={![]() }∪{
}∪{![]() }∪{
}∪{![]() }∪{-
}∪{-![]() }∪{-
}∪{-![]() }={
}={![]() ,
,![]() ,
,![]() ,-
,-![]() ,-
,-![]() }.当a1∈B时,数列
}.当a1∈B时,数列![]() 中必有某数重复出现无数次;当a1B时,数列{
中必有某数重复出现无数次;当a1B时,数列{![]() }(i=1,2,3,4,5,6)均为单调数列,任意一个数在这6个数列中最多出现一次,所以数列
}(i=1,2,3,4,5,6)均为单调数列,任意一个数在这6个数列中最多出现一次,所以数列![]() 任意一项的值均未在该数列中重复出现无数次.16分
任意一项的值均未在该数列中重复出现无数次.16分


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:
【题目】f(x)是定义在R上的函数,且对任意的x、y都有f(x+y)=f(x)+f(y)﹣1成立.当x>0时,f(x)>1.
(1)若f(4)=5,求f(2);
(2)证明:f(x)在R上是增函数;
(3)若f(4)=5,解不等式f(3m2﹣m﹣2)<3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查![]() 人,并将调查情况进行整理后制成下表:
人,并将调查情况进行整理后制成下表:
年龄(岁) |
|
|
|
|
|
频数 |
|
|
|
|
|
赞成人数 |
|
|
|
|
|
(1)世界联合国卫生组织规定: ![]() 岁为青年,
岁为青年, ![]() 为中年,根据以上统计数据填写以下
为中年,根据以上统计数据填写以下![]() 列联表:
列联表:
青年人 | 中年人 | 合计 | |
不赞成 | |||
赞成 | |||
合计 |
(2)判断能否在犯错误的概率不超过![]() 的前提下,认为赞成“车柄限行”与年龄有关?
的前提下,认为赞成“车柄限行”与年龄有关?
附: 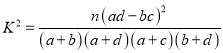 ,其中
,其中![]()
独立检验临界值表:
|
|
|
|
|
|
|
|
|
|
(3)若从年龄![]() 的被调查中各随机选取
的被调查中各随机选取![]() 人进行调查,设选中的两人中持不赞成“车辆限行”态度的人员为
人进行调查,设选中的两人中持不赞成“车辆限行”态度的人员为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为0的等差数列{an}满足:a1=1且a2 , a5 , a14成等比数列.
(1)求数列{an}的通项公式an和前n项和Sn;
(2)证明不等式 ![]() 且n∈N*)
且n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中, 曲线
中, 曲线![]() 的参数方程为
的参数方程为![]() 为参数) ;在以原点
为参数) ;在以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中, 曲线
轴的正半轴为极轴的极坐标系中, 曲线![]() 的极坐标参数方程为
的极坐标参数方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 与曲线
与曲线![]() ,
,![]() 的交点分别为
的交点分别为![]() (
(![]() 异于原点). 当斜率
异于原点). 当斜率![]() 时, 求
时, 求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+)(A,ω,是常数,A>0,ω>0)的部分图象如图所示,下列结论: ①最小正周期为π;
②将f(x)的图象向左平移 ![]() 个单位,所得到的函数是偶函数;
个单位,所得到的函数是偶函数;
③f(0)=1;
④ ![]() ;
;
⑤ ![]() .
.
其中正确的是( )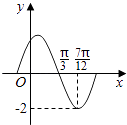
A.①②③
B.②③④
C.①④⑤
D.②③⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的二次函数f(x)=ax2﹣4bx+1
(Ⅰ)设集合P={1,2,3},集合Q={﹣1,1,2,3,4},从集合P中随机取一个数作为a,从集合Q中随机取一个数作为b,求函数f(x)在区间[1,+∞)上是增函数的概率;
(Ⅱ)设点(a,b)是区域 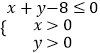 内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(﹣∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”.现有定义在(﹣∞,0)∪(0,+∞)上的如下函数:①f(x)=x2;②f(x)=2x;③f(x)= ![]() ;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
A.①②
B.③④
C.①③
D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com