
【题目】已知关于x的二次函数f(x)=ax2﹣4bx+1
(Ⅰ)设集合P={1,2,3},集合Q={﹣1,1,2,3,4},从集合P中随机取一个数作为a,从集合Q中随机取一个数作为b,求函数f(x)在区间[1,+∞)上是增函数的概率;
(Ⅱ)设点(a,b)是区域 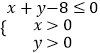 内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
【答案】解(Ⅰ)∵函数f(x)=ax2﹣4bx+1的图象的对称轴为x= ![]() ,
,
要使f(x)=ax2﹣4bx+1在区间[1,+∞)上为增函数,
当且仅当a>0且x= ![]() ≤1,
≤1,
即2b≤a.
若a=1,则b=﹣1;
若a=2,则b=﹣1,1;
若a=3,则b=﹣1,1,
∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为 ![]() .
.
(Ⅱ)由(1)知当且仅当2b≤a.且a>0时,
函数f(x)=ax2﹣4bx+1在区间[1,+∞)上为增函数,
依条件可知试验的全部结果所构成的区域为{ 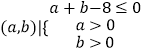 }
}
构成所求事件的区域为三角形部分.
由 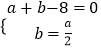 ,解得a=
,解得a= ![]() ,b=
,b= ![]() ,即交点坐标(
,即交点坐标( ![]() ,
, ![]() ),
),
∴所求事件的概率为P= 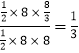
【解析】(Ⅰ)根据古典概率的概率公式进行计算即可求出概率.(Ⅱ)根据几何概型的概率公式进行计算即可.
【考点精析】根据题目的已知条件,利用二元一次不等式(组)所表示的平面区域和几何概型的相关知识可以得到问题的答案,需要掌握不等式组表示的平面区域是各个不等式所表示的平面区域的公共部;几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)讨论函数![]() 的单调性;
的单调性;
(2)函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,
两点, ![]() ,点
,点![]() 在函数
在函数![]() 的图象上,且
的图象上,且![]() 为等腰直角三角形,记
为等腰直角三角形,记 ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足:bn=an+1-an(n∈N*).
(1)若a1=1,bn=n,求数列{an}的通项公式;
(2)若bn+1bn-1=bn(n≥2),且b1=1,b2=2.
(ⅰ)记cn=a6n-1(n≥1),求证:数列{cn}为等差数列;
(ⅱ)若数列![]() 中任意一项的值均未在该数列中重复出现无数次,求首项a1应满足的条件.
中任意一项的值均未在该数列中重复出现无数次,求首项a1应满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A、B、C是椭圆![]() 上不同的三点,
上不同的三点,  ,C在第三象限,线段BC的中点在直线OA上。
,C在第三象限,线段BC的中点在直线OA上。
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点P在椭圆上(异于点A、B、C)且直线PB, PC分别交直线OA于M、N两点,证明![]() 为定值并求出该定值.
为定值并求出该定值.
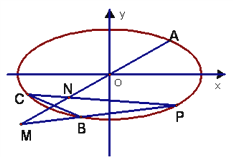
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是
支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是![]() .单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:
.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:
![]() :恰有四支球队并列第一名为不可能事件;
:恰有四支球队并列第一名为不可能事件; ![]() :有可能出现恰有两支球队并列第一名;
:有可能出现恰有两支球队并列第一名;
![]() :每支球队都既有胜又有败的概率为
:每支球队都既有胜又有败的概率为![]() ;
; ![]() :五支球队成绩并列第一名的概率为
:五支球队成绩并列第一名的概率为![]() .
.
其中真命题是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]() C.
C. ![]() .
.![]() .
.![]() D.
D. ![]() .
.![]() .
.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)= ![]() sin(2x﹣
sin(2x﹣ ![]() )+1的图象向左平移
)+1的图象向左平移 ![]() 个单位长度,再向下平移1个单位长度后,得到函数g(x)的图象,则函数g(x)具有的性质(填入所有正确的序号) ①最大值为
个单位长度,再向下平移1个单位长度后,得到函数g(x)的图象,则函数g(x)具有的性质(填入所有正确的序号) ①最大值为 ![]() ,图象关于直线x=
,图象关于直线x= ![]() 对称;②在(﹣
对称;②在(﹣ ![]() ,0)上单调递增,且为偶函数;③最小正周期为π;④图象关于点(
,0)上单调递增,且为偶函数;③最小正周期为π;④图象关于点( ![]() ,0)对称,⑤在(0,
,0)对称,⑤在(0, ![]() )上单调递增,且为奇函数.
)上单调递增,且为奇函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A={0,1,2,4},B={ ![]() ,0,1,2,6,8},则下列对应关系能构成A到B的映射的是( )
,0,1,2,6,8},则下列对应关系能构成A到B的映射的是( )
A.f:x→x3﹣1
B.f:x→(x﹣1)2
C.f:x→2x﹣1
D.f:x→2x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com