
【题目】![]() 支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是
支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是![]() .单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:
.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:
![]() :恰有四支球队并列第一名为不可能事件;
:恰有四支球队并列第一名为不可能事件; ![]() :有可能出现恰有两支球队并列第一名;
:有可能出现恰有两支球队并列第一名;
![]() :每支球队都既有胜又有败的概率为
:每支球队都既有胜又有败的概率为![]() ;
; ![]() :五支球队成绩并列第一名的概率为
:五支球队成绩并列第一名的概率为![]() .
.
其中真命题是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]() C.
C. ![]() .
.![]() .
.![]() D.
D. ![]() .
.![]() .
.![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查![]() 人,并将调查情况进行整理后制成下表:
人,并将调查情况进行整理后制成下表:
年龄(岁) |
|
|
|
|
|
频数 |
|
|
|
|
|
赞成人数 |
|
|
|
|
|
(1)世界联合国卫生组织规定: ![]() 岁为青年,
岁为青年, ![]() 为中年,根据以上统计数据填写以下
为中年,根据以上统计数据填写以下![]() 列联表:
列联表:
青年人 | 中年人 | 合计 | |
不赞成 | |||
赞成 | |||
合计 |
(2)判断能否在犯错误的概率不超过![]() 的前提下,认为赞成“车柄限行”与年龄有关?
的前提下,认为赞成“车柄限行”与年龄有关?
附: 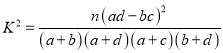 ,其中
,其中![]()
独立检验临界值表:
|
|
|
|
|
|
|
|
|
|
(3)若从年龄![]() 的被调查中各随机选取
的被调查中各随机选取![]() 人进行调查,设选中的两人中持不赞成“车辆限行”态度的人员为
人进行调查,设选中的两人中持不赞成“车辆限行”态度的人员为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+)(A,ω,是常数,A>0,ω>0)的部分图象如图所示,下列结论: ①最小正周期为π;
②将f(x)的图象向左平移 ![]() 个单位,所得到的函数是偶函数;
个单位,所得到的函数是偶函数;
③f(0)=1;
④ ![]() ;
;
⑤ ![]() .
.
其中正确的是( )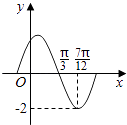
A.①②③
B.②③④
C.①④⑤
D.②③⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的二次函数f(x)=ax2﹣4bx+1
(Ⅰ)设集合P={1,2,3},集合Q={﹣1,1,2,3,4},从集合P中随机取一个数作为a,从集合Q中随机取一个数作为b,求函数f(x)在区间[1,+∞)上是增函数的概率;
(Ⅱ)设点(a,b)是区域 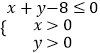 内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C方程为 ![]() (a>b>0),左、右焦点分别是F1 , F2 , 若椭圆C上的点P(1,
(a>b>0),左、右焦点分别是F1 , F2 , 若椭圆C上的点P(1, ![]() )到F1 , F2的距离和等于4. (Ⅰ)写出椭圆C的方程和焦点坐标;
)到F1 , F2的距离和等于4. (Ⅰ)写出椭圆C的方程和焦点坐标;
(Ⅱ)设点Q是椭圆C的动点,求线段F1Q中点T的轨迹方程;
(Ⅲ)直线l过定点M(0,2),且与椭圆C交于不同的两点A,B,若∠AOB为锐角(O为坐标原点),求直线l的斜率k0的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的方程为x2+y2﹣8x+15=0,若直线y=kx﹣2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程x2+y2﹣2x﹣4y+m=0.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y﹣4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m;
(3)在(2)的条件下,求以MN为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(﹣∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”.现有定义在(﹣∞,0)∪(0,+∞)上的如下函数:①f(x)=x2;②f(x)=2x;③f(x)= ![]() ;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
A.①②
B.③④
C.①③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+2)+loga(3﹣x),其中0<a<1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣4,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com