
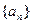 的通项公式是
的通项公式是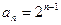 ,数列
,数列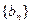 是等差数列,令集合
是等差数列,令集合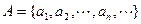 ,
,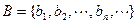 ,
,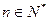 .将集合
.将集合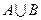 中的元素按从小到大的顺序排列构成的数列记为
中的元素按从小到大的顺序排列构成的数列记为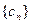 .
.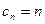 ,
,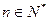 ,求数列
,求数列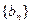 的通项公式;
的通项公式;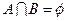 ,数列
,数列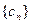 的前5项成等比数列,且
的前5项成等比数列,且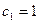 ,
,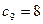 ,求满足
,求满足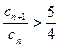
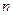 的个数.
的个数.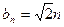 ,符合要求的
,符合要求的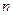 一共有5个
一共有5个
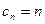 ,因为5,6,7
,因为5,6,7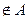 ,则5,6,7
,则5,6,7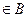 ,
,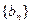 的公差为1,而3是数列
的公差为1,而3是数列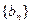 中的项,
中的项,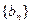 中的第1,2,3项,
中的第1,2,3项,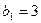 ,则
,则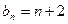 ,若
,若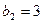 ,则
,则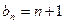 ,
, ,则
,则 ;
;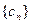 的第2项,由
的第2项,由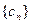 的前5项成等比数列,得
的前5项成等比数列,得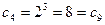 ,这显然不可能;
,这显然不可能;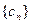 的第3项,由
的第3项,由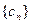 的前5项成等比数列,得
的前5项成等比数列,得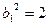 ,
,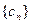 是将集合
是将集合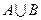 中的元素按从小到大的顺序排列构成的,
中的元素按从小到大的顺序排列构成的,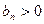 ,则
,则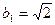 ,因此数列
,因此数列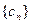 的前5项分别为1,
的前5项分别为1,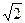 ,2,
,2,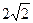 ,4,
,4,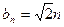 ,
,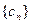 的前9项分别为1,
的前9项分别为1,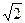 ,2,
,2,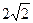 ,4,
,4,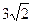 ,
,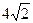 ,
,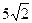 ,8,
,8,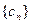 的第
的第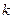 项(
项(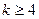 ),则
),则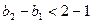 ,
,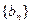 的公差
的公差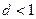 ,
,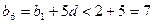 ,1,2,4<
,1,2,4<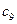 ,所以1,2,4在数列
,所以1,2,4在数列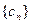 的
的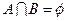 ,这样,
,这样,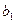 ,
,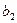 ,…,
,…,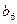 以及1,2,4共9项,
以及1,2,4共9项,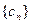 的前9项均小于8,这与
的前9项均小于8,这与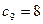 矛盾。
矛盾。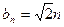 ,
,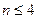 时,
时,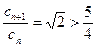 ,
,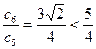 ,
,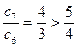 ,
, 时,
时,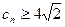 ,因为
,因为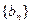 是公差为
是公差为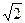 的等差数列,
的等差数列,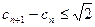 ,
,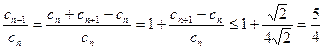 ,
,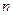 不符合要求。所以符合要求的
不符合要求。所以符合要求的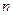 一共有5个
一共有5个


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源:不详 题型:解答题
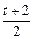 处取得最小值-
处取得最小值-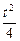 (t>0),f(1)=0.
(t>0),f(1)=0.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
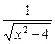 (x<-2).
(x<-2).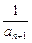 =-f--1(an)(n∈N*),求an;
=-f--1(an)(n∈N*),求an;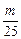 成立?若存在,求出m的值;若不存在,说明理由.
成立?若存在,求出m的值;若不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com