
已知函数f(x)=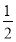 ax2-(2a+1)x+2ln x,a∈R.
ax2-(2a+1)x+2ln x,a∈R.
(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2)求f(x)的单调区间.
(1)a=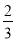 (2)f(x)的单调递增区间是
(2)f(x)的单调递增区间是 和(2,+∞),单调递减区间是
和(2,+∞),单调递减区间是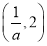
【解析】f′(x)=ax-(2a+1)+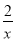 (x>0).
(x>0).
(1)由题意得f′(1)=f′(3),解得a=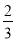 .
.
(2)f′(x)= (x>0).
(x>0).
①当a≤0时,x>0,ax-1<0.在区间(0,2)上,f′(x)>0;在区间(2,+∞)上,f′(x)<0,故f(x)的单调递增区间是(0,2),单调递减区间是(2,+∞).
②当0<a< 时,
时,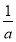 >2.在区间(0,2)和
>2.在区间(0,2)和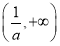 上,f′(x)>0;在区间
上,f′(x)>0;在区间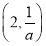 上,f′(x)<0.
上,f′(x)<0.
故f(x)的单调递增区间是(0,2)和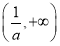 ,单调递减区间是
,单调递减区间是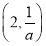 .
.
③当a=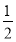 时,f′(x)=
时,f′(x)= ≥0,
≥0,
故f(x)的单调递增区间是(0,+∞).
④当a>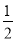 时,0<
时,0<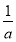 <2,在区间
<2,在区间 和(2,+∞)上,f′(x)>0;在区间
和(2,+∞)上,f′(x)>0;在区间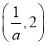 上,f′(x)<0.
上,f′(x)<0.
故f(x)的单调递增区间是 和(2,+∞),单调递减区间是
和(2,+∞),单调递减区间是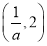 .
.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷2练习卷(解析版) 题型:解答题
在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos C+(cos A-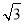 sin A)cos B=0.
sin A)cos B=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练x4-1练习卷(解析版) 题型:填空题
如图,点A、B、C都在⊙O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长为________.
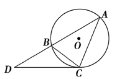
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(解析版) 题型:解答题
已知函数f(x)=ex-ln(x+m).
(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(2)当m≤2时,证明f(x)>0.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(解析版) 题型:选择题
已知f(x)是定义在(0,+∞) 上的非负可导函数,且满足xf′(x)+f(x)≤0,对任意的0<a<b,则必有( ).
A.af(b)≤bf(a) B.bf(a)≤af(b)
C.af(a)≤f(b) D.bf(b)≤f(a)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练4练习卷(解析版) 题型:选择题
已知函数y=f(x)是定义在R上的奇函数,且当x<0时,不等式f(x)+xf′(x)<0成立,若a=30.3f(30.3),b=logπ3f(logπ3),c=log3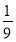 f
f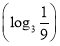 ,则a,b,c间的大小关系是( ).
,则a,b,c间的大小关系是( ).
A.a>b>c B.c>b>a
C.c>a>b D.a>c>b
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练3练习卷(解析版) 题型:解答题
已知函数f(x)=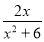 .
.
(1)若f(x)>k的解集为{x|x<-3,或x>-2},求k的值;
(2)对任意x>0,f(x)≤t恒成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练2练习卷(解析版) 题型:选择题
函数f(x)=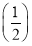 x-sin x在区间[0,2π]上的零点个数为( ).
x-sin x在区间[0,2π]上的零点个数为( ).
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-1直线与圆练习卷(解析版) 题型:选择题
过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的方程是 ( ).
A.(x-3)2+(y+1)2=4 B.(x+3)2+(y-1)2=4
C.(x-1)2+(y-1)2=4 D.(x+1)2+(y+1)2=4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com