
分析 先求出x>0,f(x)=$\frac{{e}^{x}}{x}$-1的最小值,根据奇函数的性质,即可得出结论.
解答 解:先求出x>0,f(x)=$\frac{{e}^{x}}{x}$-1的最小值,
f′(x)=$\frac{{e}^{x}(x-1)}{{x}^{2}}$,∴x∈(0,1),f′(x)<0,函数单调递减,x∈(1,+∞),f′(x)>0,函数单调递增,
∴x=1时,函数取得极小值也即最小值e-1,
∴h(x)的最大值为1-e,
故答案为1-e.
点评 本题考查奇函数的性质,考查导数知识的运用,先求出x>0,f(x)=$\frac{{e}^{x}}{x}$-1的最小值是关键.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:选择题
| A. | 一$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,6) | B. | (1,2) | C. | (-1,3) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinα>0 | B. | cosα>0 | C. | sin2α<0 | D. | cos2α<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
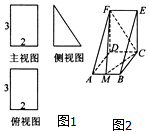 一个多面体的直观图和三视图如图所示,M是AB的 中点,一只蜜蜂在该几何体内自由飞舞,则它飞入几 何体F-AMCD内的概率为( )
一个多面体的直观图和三视图如图所示,M是AB的 中点,一只蜜蜂在该几何体内自由飞舞,则它飞入几 何体F-AMCD内的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
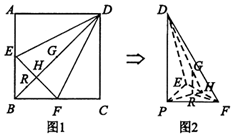 如图1,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF交于点H,G为BD中点,点R在线段BH上,且$\frac{BR}{RH}$=λ(λ>0).现将△AED,△CFD,△DEF分别沿DE,DF,EF折起,使点A,C重合于点B(该点记为P),如图2所示.
如图1,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF交于点H,G为BD中点,点R在线段BH上,且$\frac{BR}{RH}$=λ(λ>0).现将△AED,△CFD,△DEF分别沿DE,DF,EF折起,使点A,C重合于点B(该点记为P),如图2所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com