
分析 (Ⅰ)求导,利用极值点的性质知f'(a)=0,f'(b)=0,且a≠b,结合韦达定理得出结论.
(Ⅱ)对g(x)求导,结合(1)的结论a+b=t,ab=3,利用导函数进行判断即可
(Ⅲ)利用导函数得出原函数的单调性,利用极值点模拟函数,方程g(x)-m=0(x≤0)有两个不等的实根,m=g(x)有两个不同交点,进而得出m的取值范围.
解答 (Ⅰ)证明:f'(x)=x-t+$\frac{3}{x}$=$\frac{{x}^{2}-tx+3}{x}$,
∵a、b为f(x)的极值点,
∴a+b=t,ab=3.
又∵函数的定义域为(0,+∞),
∴a>0,b>0,且a≠b,不妨设b>a,
∵ab=3,
∴0<a<$\sqrt{3}$<b.
(Ⅱ)当x∈(-b,-$\sqrt{3}$)和(-$\sqrt{3}$,-a)时,g'(x)>0,g(x)递增.
证明:g'(x)=-2$\frac{({x}^{2}+tx+3)}{({x}^{2}-3)^{2}}$,
∵a+b=t,ab=3,
∴g'(x)=-2$\frac{({x}^{2}+tx+3)}{({x}^{2}-3)^{2}}$=-2$\frac{(x+a)(x+b)}{({x}^{2}-3)^{2}}$,
∵0<a<$\sqrt{3}$<b,
∴-b<-$\sqrt{3}$<-a<0,
∴当x∈(-b,-$\sqrt{3}$)和(-$\sqrt{3}$,-a)时,g'(x)>0,g(x)递增.
(Ⅲ)∵在x=1处的切线斜率为-4,
∴g'(1)=-4,
∴t=4.
∴g'(x)=-2$\frac{(x+1)(x+3)}{({x}^{2}-3)^{2}}$
∵g(-1)=-1,g(-3)=-$\frac{1}{3}$,
当x∈(-∞,-3)递减,(-3,-$\sqrt{3}$)递增,(-$\sqrt{3}$,-1)递增,(-1,+∞递减),
方程g(x)-m=0(x≤0)有两个不等的实根,
∴m=g(x)有两个不同交点,
∴m的范围为(-$\frac{1}{3}$,0)或m<-1.
点评 考查了导函数利用和韦达定理以及利用极值点模拟函数;难点是利用导函数的正负模拟函数的单调性,结合函数图象分析解决问题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<-2 | B. | m<-2.5 | C. | m<1.5 | D. | m>1.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
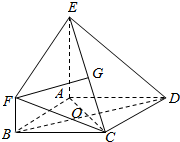 在如图所示的几何体中,底面ABCD是边长为2的菱形,∠ABC=60°,EA⊥平面ABCD,EA∥BF,EA=2BF=2,G为CE的中点,直线AC与BD相交于点O
在如图所示的几何体中,底面ABCD是边长为2的菱形,∠ABC=60°,EA⊥平面ABCD,EA∥BF,EA=2BF=2,G为CE的中点,直线AC与BD相交于点O查看答案和解析>>
科目:高中数学 来源: 题型:解答题
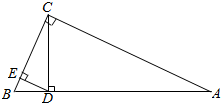 如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥BC于E,若AD=$\frac{3}{2}$$\sqrt{10}$,BE=2.求BC的长.
如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥BC于E,若AD=$\frac{3}{2}$$\sqrt{10}$,BE=2.求BC的长.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | F=G | B. | F⊆G | C. | G⊆F | D. | F∪G=G |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com