
分析 (1)由不等式f(x)≤0的解集有且只有一个元素得△=0,解得a=0或a=4.对a分类讨论,利用二次函数的单调性即可得出.
(2)由(1)知:${S_n}={n^2}-4n+4$.当n=1时,a1=S1.当n≥2时,an=Sn-Sn-1.即可得出.
(3)由(2)及其已知可得bn,cn,Tn,再利用数列的单调性即可得出.
解答 解:(1)由不等式f(x)≤0的解集有且只有一个元素得△=a2-4a=0,
解得a=0或a=4.
当a=0时,f(x)=x2在(0,+∞)上单调递增,故不存在0<x1<x2,使得不等式f(x1)>f(x2)成立;
当a=4时,f(x)=x2-4x+4在(0,2)上单调递减,故存在0<x1<x2,使得不等式f(x1)>f(x2)成立.
综上,f(x)=x2-4x+4.
(2)由(1)知:${S_n}={n^2}-4n+4$.
当n=1时,a1=S1=1.
当n≥2时,an=Sn-Sn-1=(n2-4n+4)-[(n-1)2-4(n-1)+4]=2n-5.
∴an=$\left\{\begin{array}{l}1,n=1\\ 2n-5,n≥2.\end{array}\right.$.
(3)∵${b_n}={(\sqrt{3})^{{a_n}+5}}$=$\left\{\begin{array}{l}27,n=1\\{3^n},n≥2.\end{array}\right.$,∴b1=27,b2=9,${c_1}=18-\frac{2}{27}$,
∴当n≥2时,${c_n}=\frac{{6×{3^{2n}}+{3^{n+1}}-{3^n}}}{{{3^n}×{3^{n+1}}}}$=$2+2{(\frac{1}{3})^{n+1}}$,
∴当n≥2时,${T_n}=18-\frac{2}{27}+2(n-1)+2\frac{{\frac{1}{27}(1-{{(\frac{1}{3})}^{n-1}})}}{{1-\frac{1}{3}}}$$16+\frac{1}{27}+2n-{(\frac{1}{3})^{n+1}}$,
Tn>2n+t对n∈N,n≥2恒成立等价于t<$16+\frac{1}{27}-{(\frac{1}{3})^{n+1}}$对n∈N,n≥2恒成立,
而$16+\frac{1}{27}-{(\frac{1}{3})^{n+1}}$是关于n的增函数,∴当n=2时,(Tn)min=16,
∴实数t的取值范围是t<16.
点评 本题考查二次函数的单调性、数列的递推关系、等比数列的通项公式与求和公式、不等式的解法、等价问题转化方法,考查了推理能力与计算能力,属于难题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 0户 | B. | 34户 | C. | 42户 | D. | 358户 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆的中心在原点,其左焦点F1与抛物线y2=-4x的焦点重合,过点F1的直线l与椭圆交于A,B两点,与抛物线交于C,D两点,当直线l与x轴垂直时,$\frac{|CD|}{|AB|}$=2$\sqrt{2}$.
如图,椭圆的中心在原点,其左焦点F1与抛物线y2=-4x的焦点重合,过点F1的直线l与椭圆交于A,B两点,与抛物线交于C,D两点,当直线l与x轴垂直时,$\frac{|CD|}{|AB|}$=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对于任意的角α、β都成立 | B. | 只对α、β取几个特殊值时成立 | ||
| C. | 对于任意的角α、β都不成立 | D. | 有无限个α、β的值使等式成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 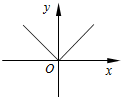 | B. | 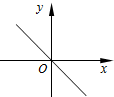 | C. | 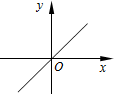 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
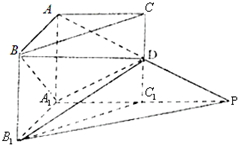 如图,在直三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连结AP交棱CC1于点D.求:
如图,在直三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连结AP交棱CC1于点D.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
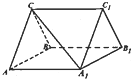 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com