
分析 (I)当φ∈$(-\frac{π}{4},\frac{π}{4})$,|OB|+|OC|=4cos(φ+$\frac{π}{4}$)+4cos(φ-$\frac{π}{4}$),展开可与$\sqrt{2}$|OA相等|.φ∈$[\frac{π}{4},\frac{π}{2})$∪$(-\frac{π}{2},-\frac{π}{4}]$时,同理可得.
(II)φ=$\frac{π}{12}$时,ρB=$4cos\frac{π}{3}$,ρC=4cos$(-\frac{π}{6})$,φ+$\frac{π}{4}$-(φ-$\frac{π}{4}$)=$\frac{π}{2}$.利用直角三角形面积计算公式即可得出.
解答 (I)证明:当φ∈$(-\frac{π}{4},\frac{π}{4})$时,∴|OB|+|OC|=4cos(φ+$\frac{π}{4}$)+4cos(φ-$\frac{π}{4}$)=4$\sqrt{2}$cosφ=$\sqrt{2}$|OA|.
φ∈$[\frac{π}{4},\frac{π}{2})$∪$(-\frac{π}{2},-\frac{π}{4}]$时,同理可得.
(II)解:φ=$\frac{π}{12}$时,ρB=$4cos\frac{π}{3}$=2,ρC=4cos$(-\frac{π}{6})$=2$\sqrt{3}$,φ+$\frac{π}{4}$-(φ-$\frac{π}{4}$)=$\frac{π}{2}$.
∴三角形△OBC的面积=$\frac{1}{2}×2×2\sqrt{3}$=2$\sqrt{3}$.
点评 本题考查了三角函数和差公式、极坐标的应用、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
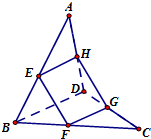 如图,E,F,G,H分别是空间四边形ABCD四边的中点.
如图,E,F,G,H分别是空间四边形ABCD四边的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6$\sqrt{3}$π | B. | 8$\sqrt{3}$π | C. | 14π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 不是充分条件,也不是必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0] | B. | [1,9] | C. | [-1,3] | D. | [-2,9] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com