
分析 (1)由频率和为1,求出a的值,根据众数的定义得出众数的值;
(2)①根据题意得出月用水量在[0,2.5]内的频率为0.75,从而得出ω的值;
②ω=2时,计算居民月用水量对应的该月人均水费即可.
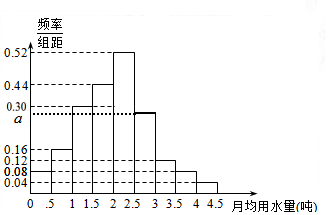
解答 解:(1)由频率分布直方图可知每段内的频率是:
[0,0.5]:0.04;(0.5,1]:0.08;(1,1.5]:0.15;
(1.5,2]:0.22; (2,2.5]:0.26; (2.5,3]:0.5a;
(3,3.5]:0.06;(3.5,4]:0.04; (4.4.5]:0.02;
则由0.04+0.08+0.15+0.22+0.26+0.5a+0.06+0.04+0.02=1,
解得a=0.26,…(2分)
众数为[2,2.5]的中点值2.25;…(4分)
(2)①由(1)可知月用水量在[0,2.5]内的频率为
0.04+0.08+0.15+0.22+0.26=0.75,
∴ω的值至少为1.25;…(6分)
②若ω=2,
当居民月用水量在[0,2]时,居民该月的人均水费为:
(0.04×0.5+0.08×1+0.15×1.5+0.22×2)×2=1.53;…(7分)
当居民月用水量在(2,2.5]时,居民该月的人均水费为:(2×2+0.5×4)×0.26=1.56,
当居民月用水量在(2.5,3]时,居民该月的人均水费为:(2×2+1×4)×0.13=1.04,
当居民月用水量在(3,3.5]时,居民该月的人均水费为:(2×2+1.5×4)×0.06=0.6,
当居民月用水量在(3.5,4]时,居民该月的人均水费为:(2×2+2×4)×0.04=0.48;…(9分)
当居民月用水量在(4,4.5]时,居民该月的人均水费为:(2×2+2×4+0.5×10)×0.02=0.34;…(10分)
∴居民月人均水费为1.53+1.56+1.04+0.6+0.48+0.34=5.55元.…(12分)
点评 本题考查了频率分布直方图的应用问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对于任意的角α、β都成立 | B. | 只对α、β取几个特殊值时成立 | ||
| C. | 对于任意的角α、β都不成立 | D. | 有无限个α、β的值使等式成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
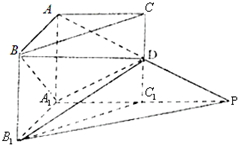 如图,在直三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连结AP交棱CC1于点D.求:
如图,在直三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连结AP交棱CC1于点D.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段.如果抽得号码有下列四种情况:
某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段.如果抽得号码有下列四种情况:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com