
 椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点分别为F1,F2,M在椭圆上,△MF1F2的周长为$2\sqrt{5}+4$,面积的最大值为2.
椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点分别为F1,F2,M在椭圆上,△MF1F2的周长为$2\sqrt{5}+4$,面积的最大值为2.分析 (I)利用△MF1F2的周长为$2\sqrt{5}+4$,面积的最大值为2.列出方程求出a,b即可得到椭圆方程.
( II)设A(x0,y0),则B(-x0,-y0).直线$AD:x=\frac{{{x_0}-2}}{y_0}y+2$,代入$C:\frac{x^2}{5}+{y^2}=1$,结合$\frac{{{x_0}^2}}{5}+{y_0}^2=1$,代入化简得$(9-4{x_0}){y^2}+4({x_0}-2){y_0}y-y_0^2=0$,设$D(x_1^{\;},{y_1}),E({x_2},{y_2})$,利用韦达定理通过斜率关系,化简求解即可.
解答 解:( I)$|{F_1}{F_2}|+|M{F_1}|+|M{F_2}|=2a+2c=2\sqrt{5}+4$,…2′,
$S=\frac{1}{2}2c•b=bc=2$,…4′
得$a=\sqrt{5},c=2,b=1$,所以$C:\frac{x^2}{5}+{y^2}=1$.…6′
(2)( II)设A(x0,y0),则B(-x0,-y0).
直线$AD:x=\frac{{{x_0}-2}}{y_0}y+2$,…8′
代入$C:\frac{x^2}{5}+{y^2}=1$得$[{{{({x_0}-2)}^2}+5y_0^2}]{y^2}+4({x_0}-2){y_0}y-y_0^2=0$,
因为$\frac{{{x_0}^2}}{5}+{y_0}^2=1$,代入化简得$(9-4{x_0}){y^2}+4({x_0}-2){y_0}y-y_0^2=0$,
设$D(x_1^{\;},{y_1}),E({x_2},{y_2})$,则${y_0}{y_1}=\frac{-y_0^2}{{9-4{x_0}}}$,
所以${y_1}=\frac{{-y_0^{\;}}}{{9-4{x_0}}}$,${x_1}=\frac{{{x_0}-2}}{y_0}{y_1}+2$.…12′
直线$BE:x=\frac{{{x_0}+2}}{y_0}y+2$,
同理可得${y_2}=\frac{{y_0^{\;}}}{{9+4{x_0}}}$,${x_2}=\frac{{{x_0}+2}}{y_0}{y_2}+2$.
所以${k_{DE}}=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{{{y_1}-{y_2}}}{{\frac{{{x_0}-2}}{y_0}{y_1}-\frac{{{x_0}+2}}{y_0}{y_2}}}=\frac{{{y_1}-{y_2}}}{{\frac{x_0}{y_0}({y_1}-{y_2})-2\frac{{{y_1}+{y_2}}}{y_0}}}=\frac{1}{{\frac{x_0}{y_0}-\frac{2}{y_0}•\frac{{{y_1}+{y_2}}}{{{y_1}-{y_2}}}}}$
=$\frac{1}{{\frac{x_0}{y_0}+-\frac{2}{y_0}•\frac{{4{x_0}}}{9}}}=9\frac{y_0}{x_0}=9k$,
所以kDE:k=9. …15′
(其他解法酌情给分)
点评 本题考查椭圆的简单性质,椭圆方程的求法,直线与椭圆的位置关系的应用,考查转化思想以及计算能力.


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-2x+2≤0 | B. | ?x0∈R,$x_0^2-2{x_0}+2>0$ | ||
| C. | ?x0∈R,$x_0^2-2{x_0}+2<0$ | D. | ?x0∈R,$x_0^2-2{x_0}+2≤0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
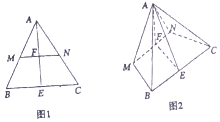 已知在边长为4的等边△ABC(如图1所示)中,MN∥BC,E为BC的中点,连接AE交MN于点F,现将△AMN沿MN折起,使得平面AMN⊥平面MNCB(如图2所示).
已知在边长为4的等边△ABC(如图1所示)中,MN∥BC,E为BC的中点,连接AE交MN于点F,现将△AMN沿MN折起,使得平面AMN⊥平面MNCB(如图2所示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com