
| 时间t | 30 | 40 | 70 | 90 | 120 |
| 成绩y | 35 | 48 | m | 82 | 92 |
科目:高中数学 来源: 题型:解答题
 某地政府调查了工薪阶层1000人的月工资收入,并根据调查结果画出如图所示的频率分布直方图,其中工资收入分组区间是[10,15),[15,20),[20,25),[25,30)[30,35),[35,40](单位:百元)
某地政府调查了工薪阶层1000人的月工资收入,并根据调查结果画出如图所示的频率分布直方图,其中工资收入分组区间是[10,15),[15,20),[20,25),[25,30)[30,35),[35,40](单位:百元)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,所有棱长都相等的直四棱柱ABCD-A′B′C′D′中B′D′中点为E′.
如图,所有棱长都相等的直四棱柱ABCD-A′B′C′D′中B′D′中点为E′.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
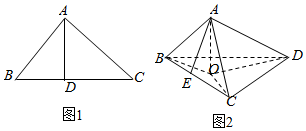 如图1所示,在△ABC中,AB⊥AC,AD⊥BC,则AB2=BD•BC.类似有命题:在三棱锥A-BCD中,如图2所示,AD⊥面ABC.若A在△BCD内的射影为O,E在BC上,且E,O,D在同一条直线上,则S△ABC2=S△BCO•S△BCD,此命题是( )
如图1所示,在△ABC中,AB⊥AC,AD⊥BC,则AB2=BD•BC.类似有命题:在三棱锥A-BCD中,如图2所示,AD⊥面ABC.若A在△BCD内的射影为O,E在BC上,且E,O,D在同一条直线上,则S△ABC2=S△BCO•S△BCD,此命题是( )| A. | 假命题 | |
| B. | 增加AB⊥AC的条件才是真命题 | |
| C. | 真命题 | |
| D. | 增加三棱锥A-BCD是正棱锥的条件才是真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com